¿Qué son las correlaciones entre variables? ¿Cómo entenderlas y trabajar con ellas? ¿Qué información nos ofrecen? ¿Cómo calcular éstas en R? En esta entrada trato el tema de la correlación, concretamente la lineal, de Pearson. Vamos a ver unos cuantos ejemplos utilizando funciones específicas de distintas librerías. En entradas posteriores veremos otros ejemplos de cálculo de correlaciones no paramétricas, como la de Spearman, o Kendall (consideradas ambas coeficientes de correlación de rango).
Puedes consultar el documento en RPubs [aquí]
Librerías utilizadas. Lenguaje utilizado, R.
library(tidyverse)
library(PerformanceAnalytics)
library(apaTables)
library(psych)
library(corrr)
library(corrplot)
library(palmerpenguins)Correlación
Para examinar si existe relación entre dos variables aleatorias estudiamos la existencia de correlación. Las relaciones entre variables pueden ser diversas y, en la correlación lineal, medimos concretamente la intensidad de la fuerza de la relación lineal entre ambas. Cuando los valores de una variable aumentan con los de otra, hablamos de la existencia de correlación positiva, o directa. Por el contrario, si el aumento de una variable resulta en la disminución de la otra, estaríamos ante una correlación negativa, o inversa.
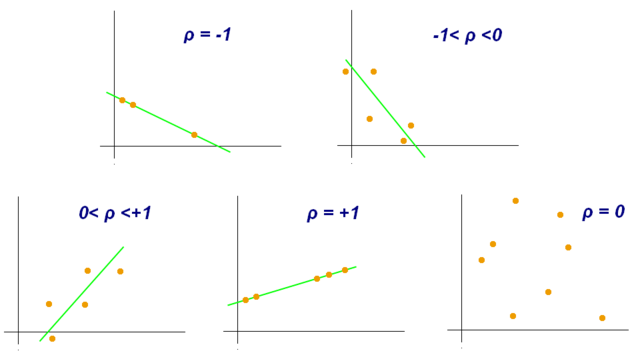
Existen coeficientes de correlación paramétricos y no paramétricos. El que usemos unos u otros va a depender de que se cumplan, o no, una serie de supuestos en nuestros datos, siendo los paramétricos los más estrictos en lo que al cumplimiento de estos requisitos se refiere. En este sentido, es importante entender que no podemos utilizar cualquier test, o coeficiente, en cualquier situación. Hay que entender bien cuando estos ofrecerían resultados válidos o, por el contrario, conclusiones erróneas. Es más habitual de lo que parece ver conclusiones basadas en resultados de unos análisis dudosos en cuanto a su planteamiento inicial, y desarrollo.
EL COEFICIENTE DE CORRELACIÓN LINEAL DE PEARSON
El coeficiente de correlación de PEARSON (r) es el más utilizado dentro de los paramétricos. Por otro lado, dentro de los no paramétricos tenemos los coeficientes de correlación por rangos de SPEARMAN y KENDALL (también conocido como Tau de Kendall).
El coeficiente de correlación de Pearson es una prueba que mide la relación LINEAL entre dos variables continuas. Este detalle es muy importante porque si la relación entre los elementos no es lineal, el coeficiente no representará adecuadamente esta relación. Y es que dos variables pueden estar correlacionadas, y estarlo de una forma no lineal.
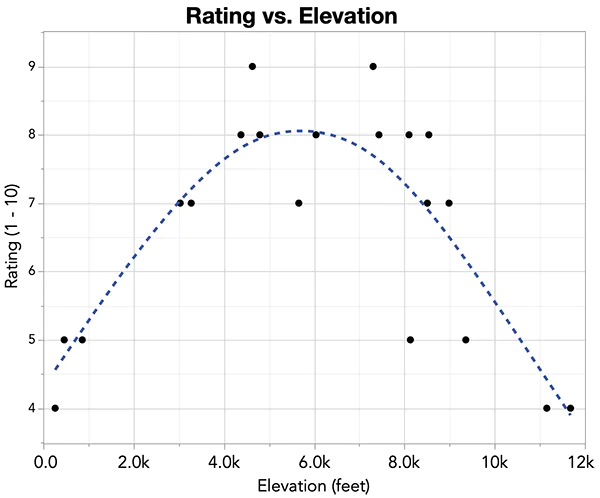
El coeficiente de Pearson mide el grado de aproximación de los puntos a lo que sería una recta que representaría la correlación máxima pero, ¿Qué ocurre si los puntos adoptan una posición dibujando una curva? En estos casos habría que utilizar otro tipo de procedimientos, en los que calcularíamos lo que conocemos como índices de razón de correlación. Aquí un ejemplo de un ajuste no lineal. Si calculáramos aquí el coeficiente de Pearson nos daría un valor bajo. Sin embargo, si existe un ajuste de los datos (puntos) a la curva.
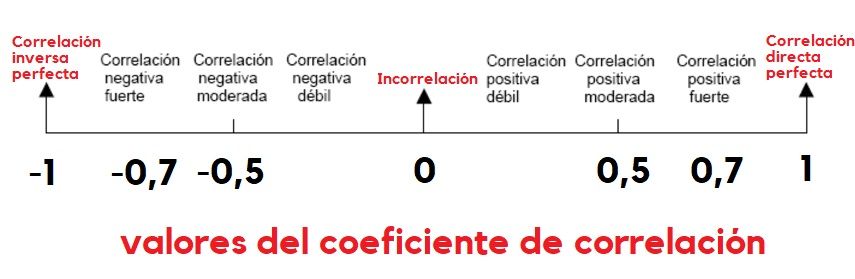
El coeficiente de correlación de Pearson puede tomar un rango de valores de -1 a +1. Estos valores extremos implicarían la existencia de una correlación perfecta (ajuste perfecto a la recta), algo que, por otro lado, es bastante raro en las ciencias más allá de la física.
Aquí un ejemplo sencillo, basado en datos reales.
Estudiamos si existe relación entre las cantidades de arsénico y nitratos medidos en muestras de lluvia ácida (datos publicados en «The atmospheric Deposition of Arsenic and Association with Acid Precipitation» Atmospheric Environ. (1988): 937-943
nitrato <- c(11, 13, 18, 30, 36, 40, 50, 58, 67, 82, 91, 102)
arsenico <- c(1.1, 0.5, 2.4, 1.2, 2.1, 1.2, 4.0, 2.3, 1.7, 3.7, 3.0, 3.9)
summary(nitrato)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 11.00 27.00 45.00 49.83 70.75 102.00summary(arsenico)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.500 1.200 2.200 2.258 3.175 4.000Las correlación entre las variables nitrato y arsénico se pueden calcular con la función cor. Igualmente podemos realizar un test para estudiar la significación de esta, con la función cor.test. Como veremos también, es posible representar gráficamente la relación entre las variables con pairs o, con la función chart.Correlation de la librería de PerformanceAnalytics. Aquí solo detallo algunas de ellas. Hay un montón de paquetes en R para realizar este tipo de cálculos y representar matrices de correlación.
correlacion <- cor(nitrato, arsenico)
cor(arsenico, nitrato) #exactamente lo mismo, de una u otra forma## [1] 0.7319313Hacemos el test para conocer si hay significación estadística en el valor de r (correlación de PEARSON obtenida). El p-valor indica la probabilidad de obtener una correlación igual o más extrema que la observada en tus datos si la verdadera correlación entre nitrato y arsénico fuera igual a cero. Este p-valor se compara con el nivel de significación típico de 0.05 (o alfa), el umbral más comúnmente utilizado. Podemos concluir que la correlación entre nitrato y arsénico es significativa. La hipótesis nula en este test es que la correlación entre las variables es igual a 0, es decir, que no existe correlación.
cor.test(nitrato, arsenico)##
## Pearson's product-moment correlation
##
## data: nitrato and arsenico
## t = 3.3969, df = 10, p-value = 0.006807
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.2724915 0.9195640
## sample estimates:
## cor
## 0.7319313Gráficamente, con las funciones mencionadas anteriormente:
pairs(nitrato ~ arsenico)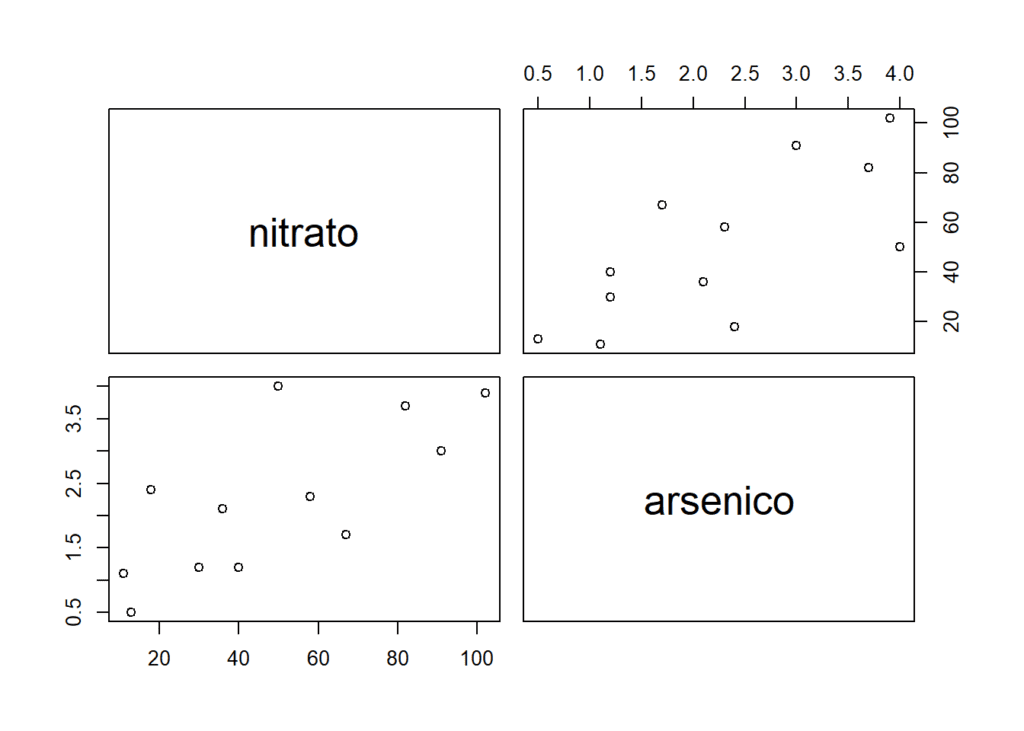
data <- data.frame(nitrato, arsenico)
chart.Correlation(data)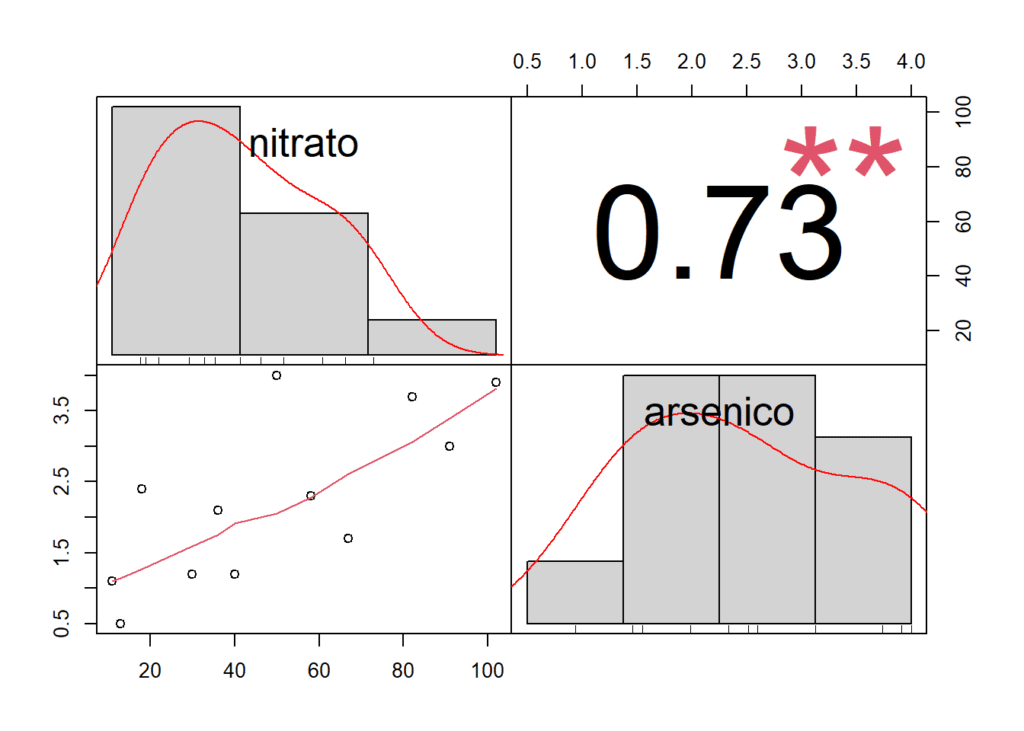
Para saber si realmente es correcto calcular un coeficiente de correlación de Pearson es necesario asegurarnos de que las variables implicadas tienen una distribución normal. Para estudiar la normalidad de los datos utilizaremos el test de SHAPIRO WILK.
En una prueba de Shapiro-Wilk la hipótesis nula (H0) es que los datos siguen una distribución normal, es decir, que no hay evidencia suficiente para concluir que los datos no siguen una distribución normal. La hipótesis alternativa (H1) sería que los datos no siguen una distribución normal.
Si el p-value (p-valor en castellano) es menor que un nivel de significancia predefinido (generalmente 0.05 o 0.01), se rechaza la hipótesis nula. Así, si el p-value es muy pequeño, se concluye que hay evidencia suficiente para afirmar que los datos no siguen una distribución normal.
shapiro.test(nitrato)##
## Shapiro-Wilk normality test
##
## data: nitrato
## W = 0.94465, p-value = 0.5605shapiro.test(arsenico)##
## Shapiro-Wilk normality test
##
## data: arsenico
## W = 0.93354, p-value = 0.4191A partir de r podemos también calcular lo que llamamos, COEFICIENTE DE DETERMINACIÓN R^2. Este nos servirá para conocer el % de variación de una variable que es explicado por la otra. En este caso es tan sencillo como elevar al cuadrado r. Así, el 53,6% de la variación de la cantidad que podemos encontrar de arsénico en la lluvia ácida está relacionada con la presencia también de arsénico. ATENCIÓN, esto no quiere decir para nada que la causa de la presencia de arsénico en la muestra se deba a que esté presente el nitrato. Aprendeos bien eso de que la correlación no implica causalidad. La causalidad habría que estudiarla aparte, en detalle y con el diseño experimental necesario para poder alcanzar conclusiones de ese estilo.
Cálculo del coeficiente de determinación
correlacion ^ 2 * 100## [1] 53.57 %Trabajando con la librería de Palmer Penguins. La librería «palmerpenguins» es una librería de datos en R que contiene información biométrica sobre pingüinos. Esta librería es útil para fines educativos y de práctica en análisis de datos y visualización en R, por lo que es conocida por mucha gente. Proporciona datos sobre diferentes especies de pingüinos, incluyendo su tamaño, peso y otras características (por ejemplo, longitud del pico).
Miramos los data que hay en la librería y cargamos el dataset que se llama penguins. Como vamos a hacer ahora una matriz de correlación, sobran todas las columnas que tienen variables no numéricas (eliminamos las columnas 1, 2 y 7, que se refieren a los nombres de las especies «species», nombres de las islas en las que se encuentran «island» y, el sexo de los animales «sex». Así, creamos un nuevo dataset (se llama en R, data frame) al que le ponemos el nombre de df_noNA y que está formado por los casos completos (que no tengan NA). Por último, creamos la matriz de correlación con la función cor.
¿Que son los NA? En el contexto de la gestión de datos, «NA» significa «Not Available» o «Not Applicable«, y se utiliza para representar valores faltantes o ausentes en un conjunto de datos. En una buena parte de análisis es necesario «eliminar» previamente estos (dicho sin entrar mucho en este tema, que es bastante complejo).
data(package = "palmerpenguins")
data(penguins)
colnames(penguins)## [1] "species" "island" "bill_length_mm"
## [4] "bill_depth_mm" "flipper_length_mm" "body_mass_g"
## [7] "sex" "year"df <- penguins[, -c(1, 2, 7)]
df_noNA <- df[complete.cases(df), ]
matrix_cor <- cor(df_noNA, method = "pearson")
matrix_cor_tres_decimales <- round(matrix_cor, digits = 3)
matrix_cor_tres_decimales## bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
## bill_length_mm 1.000 -0.235 0.656 0.595
## bill_depth_mm -0.235 1.000 -0.584 -0.472
## flipper_length_mm 0.656 -0.584 1.000 0.871
## body_mass_g 0.595 -0.472 0.871 1.000
## year 0.055 -0.060 0.170 0.042
## year
## bill_length_mm 0.055
## bill_depth_mm -0.060
## flipper_length_mm 0.170
## body_mass_g 0.042
## year 1.000Utilizando la librería apaTables para crear una tabla de correlaciones en detalle. Esta función apa.cor.table permite crear automáticamente una tabla de correlaciones entre las variables y, grabarla en un documento .doc
apa.cor.table(df_noNA, filename = "prueba.doc", table.number = 1, show.conf.interval = TRUE, landscape = TRUE)##
##
## Table 1
##
## Means, standard deviations, and correlations with confidence intervals
##
##
## Variable M SD 1 2 3
## 1. bill_length_mm 43.92 5.46
##
## 2. bill_depth_mm 17.15 1.97 -.24**
## [-.33, -.13]
##
## 3. flipper_length_mm 200.92 14.06 .66** -.58**
## [.59, .71] [-.65, -.51]
##
## 4. body_mass_g 4201.75 801.95 .60** -.47** .87**
## [.52, .66] [-.55, -.39] [.84, .89]
##
## 5. year 2008.03 0.82 .05 -.06 .17**
## [-.05, .16] [-.17, .05] [.06, .27]
##
## 4
##
##
##
##
##
##
##
##
##
##
##
## .04
## [-.06, .15]
##
##
## Note. M and SD are used to represent mean and standard deviation, respectively.
## Values in square brackets indicate the 95% confidence interval.
## The confidence interval is a plausible range of population correlations
## that could have caused the sample correlation (Cumming, 2014).
## * indicates p < .05. ** indicates p < .01.
## También, de la librería psych podemos utilizar la función pairs.panels para crear este tipo de gráficos en el que se resumen las correlaciones entre las variables, se indican si son significativas, se muestran sus distribuciones, etc.
pairs.panels(df_noNA, pch = 20, stars = TRUE, main = "Palmer Penguins")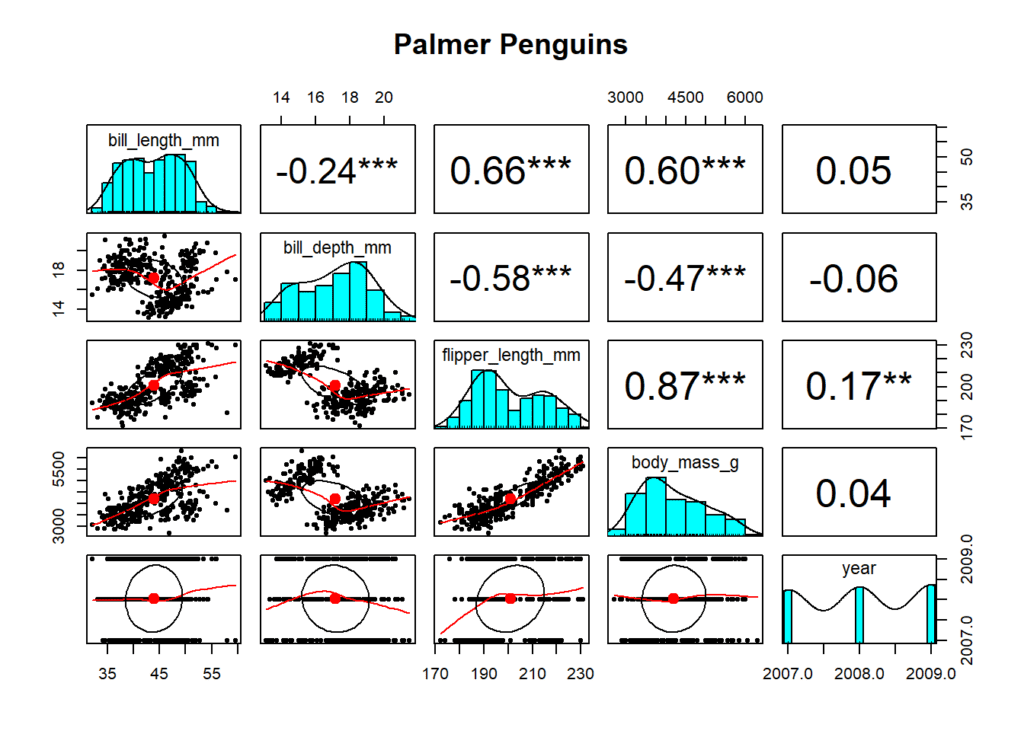
Algunos gráficos, algo más extraños …
Podemos crear una red de correlaciones con la funciones correlate & network plot de la librería corrr, en la que vemos las relaciones que hay entre unas variables y otras (en rojo las relaciones negativas y en azul las positivas)
df_noNA %>%
correlate() %>%
network_plot()## Correlation computed with
## • Method: 'pearson'
## • Missing treated using: 'pairwise.complete.obs'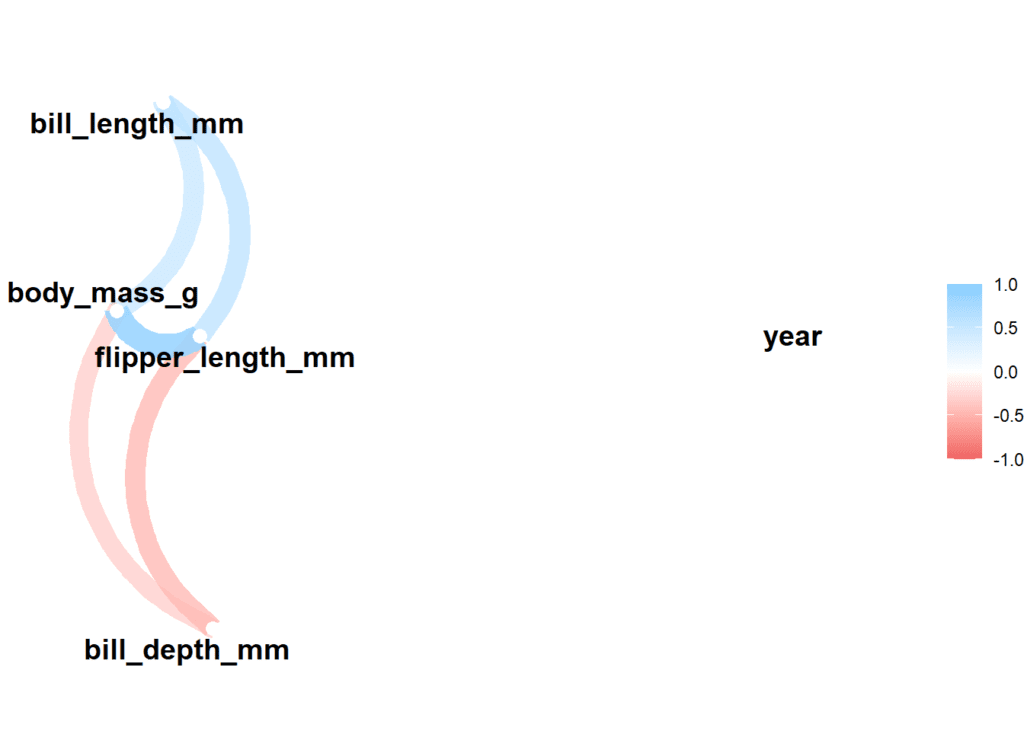
CORRPLOT
Corrplot es una de las funciones más conocidas a la hora de representar gráficamente las relaciones entre variables. Visualmente resulta bastante útil y permite personalizar el resultado final hasta un punto más que suficiente. En este ejemplo se calcula una matriz de correlación con la función corrplot. En ella se muestran las correlaciones positivas en color azul, con un círculo de mayor tamaño conforme más grande es esta correlación. En rojo, las correlaciones negativas.
corrplot(matrix_cor_tres_decimales)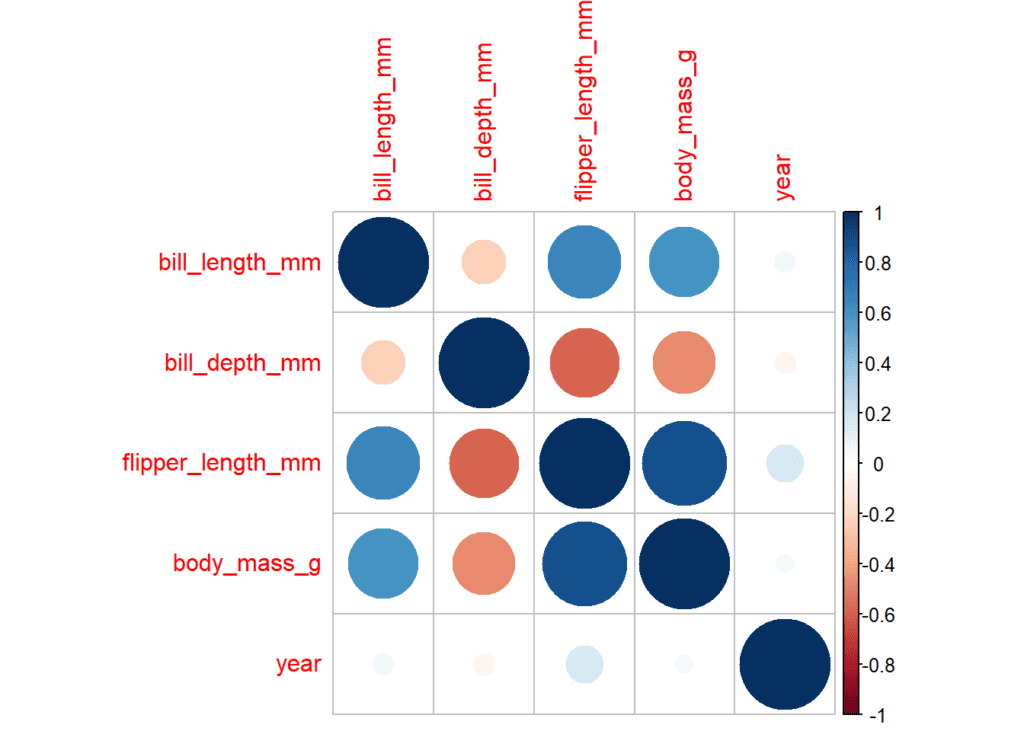
Modificando y añadiendo parámetros para personalizar el resultado
corrplot(matrix_cor_tres_decimales, method = "shade", shade.col = NA, tl.col = "black", tl.srt = 45)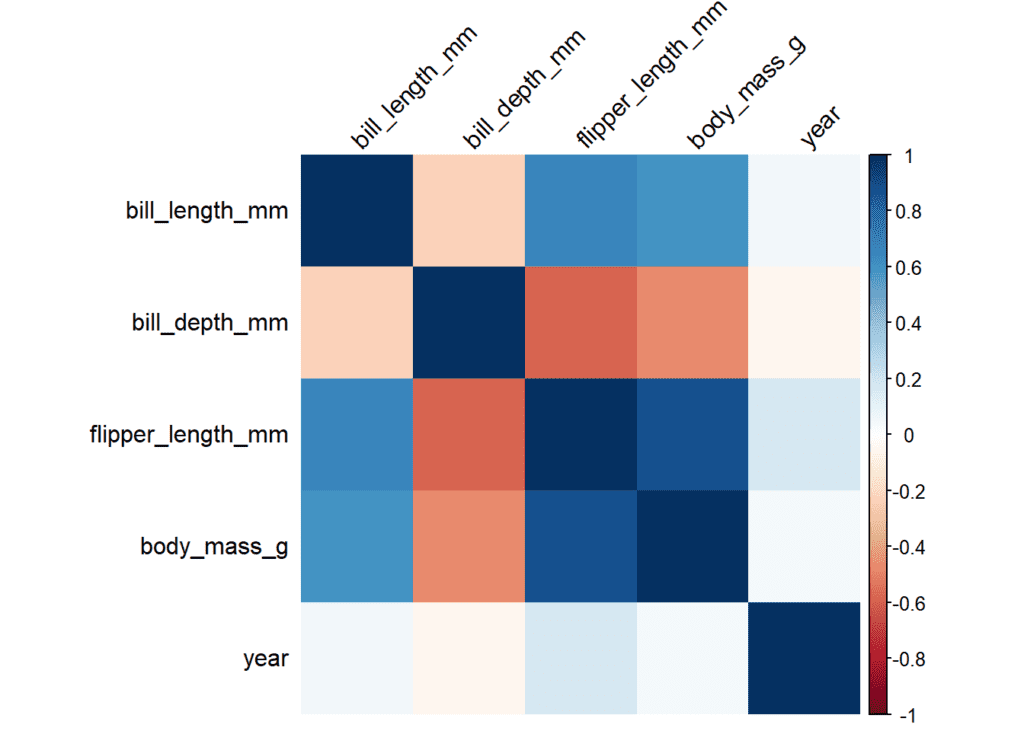
corrplot(matrix_cor_tres_decimales, method = "shade", shade.col = NA, tl.col = "black", addCoef.col = "black", tl.srt = 45, order = "AOE")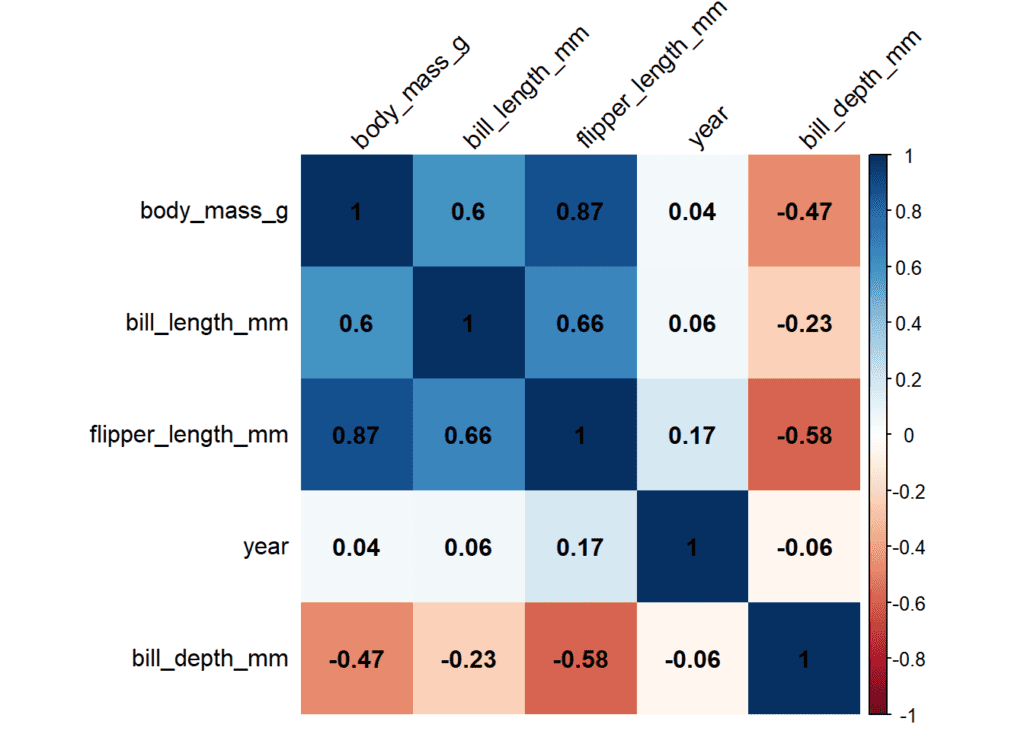
corrplot(matrix_cor_tres_decimales, insig = "p-value", sig.level = 0.05,
method = "shade", shade.col = NA, tl.col = "black",
addCoef.col = "black", tl.srt = 45,
order = "AOE", type = "lower", diag = FALSE, addshade = "all") 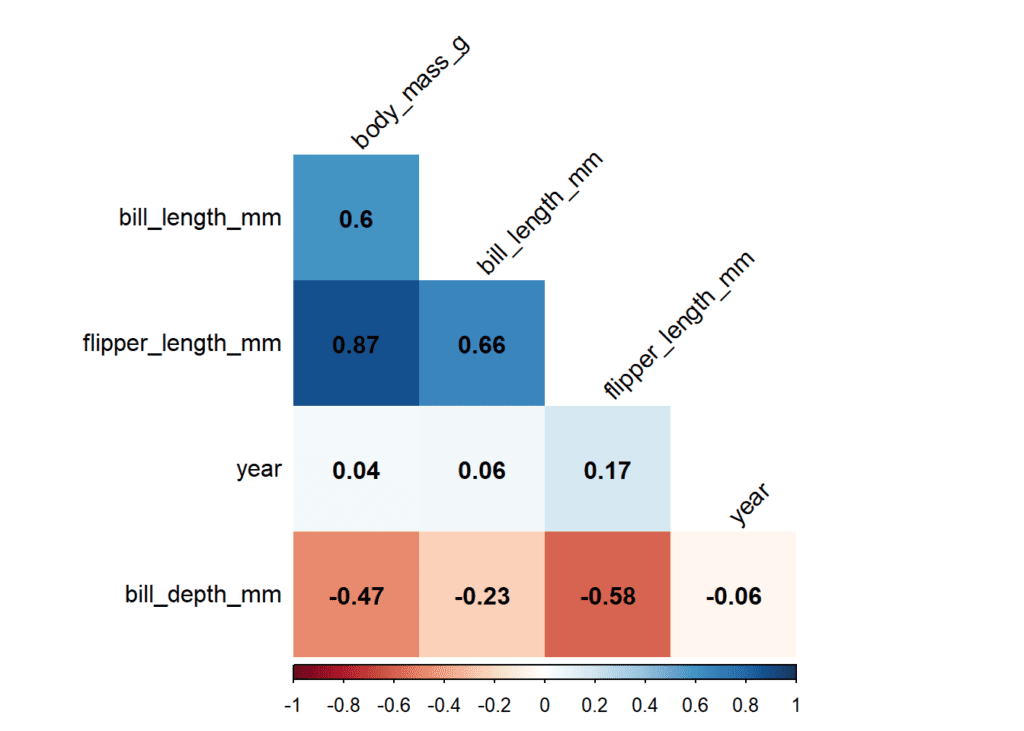
Por último, y algo más complejo, un ejemplo con el dataset de mtcars, y las diversas opciones de corrplot. Utilizando la función cor.mtest es posible calcular los valores de significación de las correlaciones según el nivel de confianza que le indiquemos (en este caso 0.95). Creará una columna llamada p con estos valores. Luego en corrplot es posible añadir los parámetros p.mat y sig.level para que se marquen como «tachadas» las correlaciones que no son significativas.
data(mtcars)
mtcars.cor <- cor(mtcars)
mtcars.sig <- cor.mtest(mtcars, conf.level = 0.95)
corrplot(mtcars.cor, p.mat = mtcars.sig$p, sig.level = 0.05, method = "color", order = "hclust", type = "lower", diag = FALSE, addCoef.col = "black", number.cex = 0.6)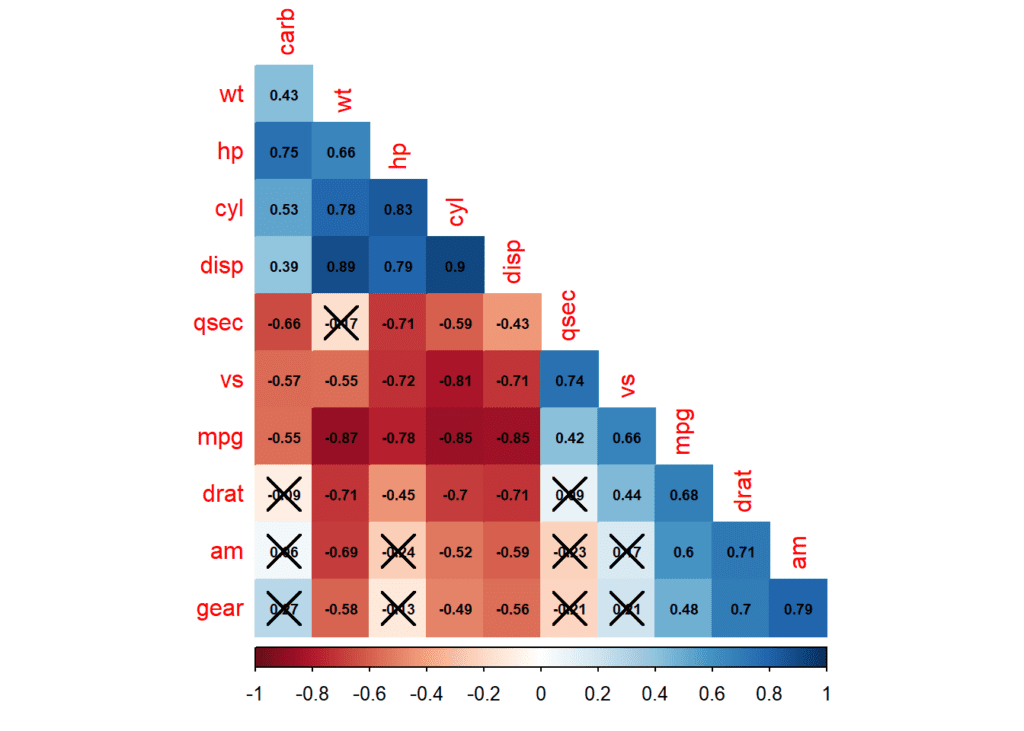
end of file…
