📊 Analizando las diferencias de ventas por región con ANOVA en R: ¿Dónde se vende más?

Data Science – Supuesto práctico de programación en R y aplicación de ANOVA unifactorial

En el mundo actual de los negocios, los datos son uno de los activos más valiosos que tenemos. Pero tener datos no basta: la clave está en saber interpretarlos correctamente para tomar decisiones informadas. Por eso, en esta sencilla práctica de introducción voy a mostrar paso a paso cómo aplicar una técnica estadística fundamental llamada ANOVA unifactorial, con un ejemplo relacionado con las ventas en distintas regiones.

El objetivo no es solo mostrar la teoría, sino también hacerla accesible y útil para quienes trabajan con datos en áreas comerciales y de marketing. A través de esta práctica, quiero demostrar cómo podemos identificar si las diferencias que vemos en nuestros números —por ejemplo, las ventas entre distintas zonas geográficas— son realmente significativas o si podrían ser producto del azar.

Además, iremos desgranando cada paso del proceso: desde la generación de datos simulados, la comprobación de supuestos estadísticos, hasta la interpretación de los resultados. La intención es ofrecer una primera aproximación a este tipo de análisis, que luego iremos enriqueciendo con casos de mayor complejidad.

Utilizaremos el lenguaje de programación R, una herramienta poderosa y muy popular en el mundo del análisis y la ciencia de datos. Veremos cómo podemos utilizar R para crear nuestros propios conjuntos de datos, realizar los análisis estadísticos y generar gráficos que nos ayuden a visualizar los resultados. No se trata solo de hacer números, sino de entender qué significan y cómo mostrarlos de forma clara y efectiva.

En definitiva, esta práctica es una invitación a entender mejor el poder y los límites del análisis estadístico en el mundo real, y cómo, con un poco de conocimiento y las herramientas adecuadas, podemos convertir los datos en decisiones que realmente marcan la diferencia.

En el mundo de los negocios, tomar decisiones basadas en datos es más importante que nunca. Imagina que una empresa cuenta con varios equipos comerciales distribuidos en distintas regiones: Norte, Centro y Sur. Cada equipo reporta sus ventas mensuales, y la dirección comercial se enfrenta a una pregunta clave:

¿Las diferencias en ventas entre regiones son estadísticamente significativas, o se deben simplemente al azar?

Responder a esta pregunta no es solo una cuestión de curiosidad. Si una región vende sistemáticamente más que otra, podría deberse a factores como:

• mejor rendimiento del equipo comercial,
• diferencias en el potencial de mercado,
• estrategias de ventas más efectivas,
• u otros factores operativos o de contexto.

🧩 Cuidado. Lo que parece obvio… no siempre lo es

— «Viendo los datos, está claro que en esta zona se vende menos, ¿no? Para eso no hace falta hacer estadística.»

Esa es una frase habitual cuando mostramos un gráfico de barras o una tabla de medias. Y tiene sentido: a simple vista, una diferencia de 4.000 o 5.000 euros entre regiones parece suficiente como para darla por hecha.

Pero aquí es donde entra la parte interesante.

🧠 El problema de confiar solo en lo que “parece”

Cuando trabajamos con datos reales —como ventas mensuales, ingresos por comercial, o rendimiento por zona— siempre existe una variabilidad natural. Un mes fuerte, una promoción puntual, un cliente grande que hace un pedido atípico… y de pronto, una media se dispara o se desploma.

Entonces surge la pregunta clave:

¿Esa diferencia entre regiones es real, o simplemente fruto del azar?

📊 Aquí es donde utilizar la estadística tiene sentido

El análisis ANOVA (y en concreto el test de Tukey que aplicamos después) no solo mira los promedios, sino también cuánta variación hay dentro de cada grupo. Nos ayuda a responder preguntas como:

• ¿La diferencia entre regiones supera lo que podría esperarse por casualidad?
• ¿Las ventas del sur están realmente por debajo, o es solo una mala racha?
• ¿Tiene sentido intervenir ahí, o estamos reaccionando a ruido?

Y nos da una respuesta sólida, basada en evidencia, no en intuiciones.

🎯 Porque tomar decisiones cuesta dinero

Imagínate tomar acciones basadas en una diferencia “que parecía grande”:

• Rediseñar el plan comercial de una zona.
• Aumentar presupuesto publicitario.
• Cambiar responsables regionales.

¿Y si después resulta que no había una diferencia real? La estadística no solo nos da confianza, también nos ahorra errores caros.

🧠 ¿Qué es ANOVA y para qué sirve en ventas?

ANOVA (Analysis of Variance) es una técnica que permite comparar las medias de un mismo indicador entre más de dos grupos. En este caso, el indicador es el volumen de ventas, y los grupos son las tres regiones.

A diferencia de una simple comparación por pares (como una t de Student entre las regiones NORTE y CENTRO, etc), ANOVA permite evaluar todas las regiones al mismo tiempo y determinar si, globalmente, existen diferencias estadísticamente significativas.

📊 Otros ejemplos prácticos de uso del ANOVA

1. Ventas por región o canal de distribución

Comparar si existen diferencias significativas en las ventas medias entre distintas regiones (norte, centro, sur) o entre diferentes canales (online, tienda física, distribuidores).

2. Impacto de campañas publicitarias

Evaluar si las ventas medias cambian según el tipo de campaña (televisión, redes sociales, email marketing). ANOVA ayuda a saber si una estrategia funciona mejor que otra.

3. Satisfacción del cliente por tienda

Analizar si la media de satisfacción de clientes varía entre varias sucursales de una empresa. Si hay diferencias, podría ser necesario revisar la gestión o el servicio en ciertos puntos.

4. Comparación de productividad entre equipos

Estimar si hay diferencias estadísticamente significativas en la productividad media entre diferentes equipos o departamentos dentro de una empresa.

5. Efecto del precio sobre la intención de compra

Estudiar si diferentes niveles de precio afectan de manera significativa la media de intención de compra de los consumidores (por ejemplo, precio bajo, medio y alto).

6. Tiempo medio de respuesta entre centros de atención al cliente

Comparar si los tiempos de respuesta a los clientes varían significativamente entre varios centros de soporte técnico o call centers.

7. Coste medio por proveedor

Determinar si distintos proveedores tienen diferencias significativas en los costes medios de adquisición para una misma materia prima.

8. Diferencia en rendimiento por tipo de formación

Medir si el rendimiento de los empleados (por ejemplo, en una evaluación interna) cambia según el tipo de formación recibida (presencial, online, tutoría personalizada).

9. Engagement por tipo de contenido

Analizar si el tipo de contenido (vídeo, artículo, infografía) influye en la media de tiempo de permanencia de usuarios en una web o app.

10. Eficacia de distintos procesos productivos

Comparar la media de defectos en productos según tres métodos de producción diferentes para elegir el más eficiente.

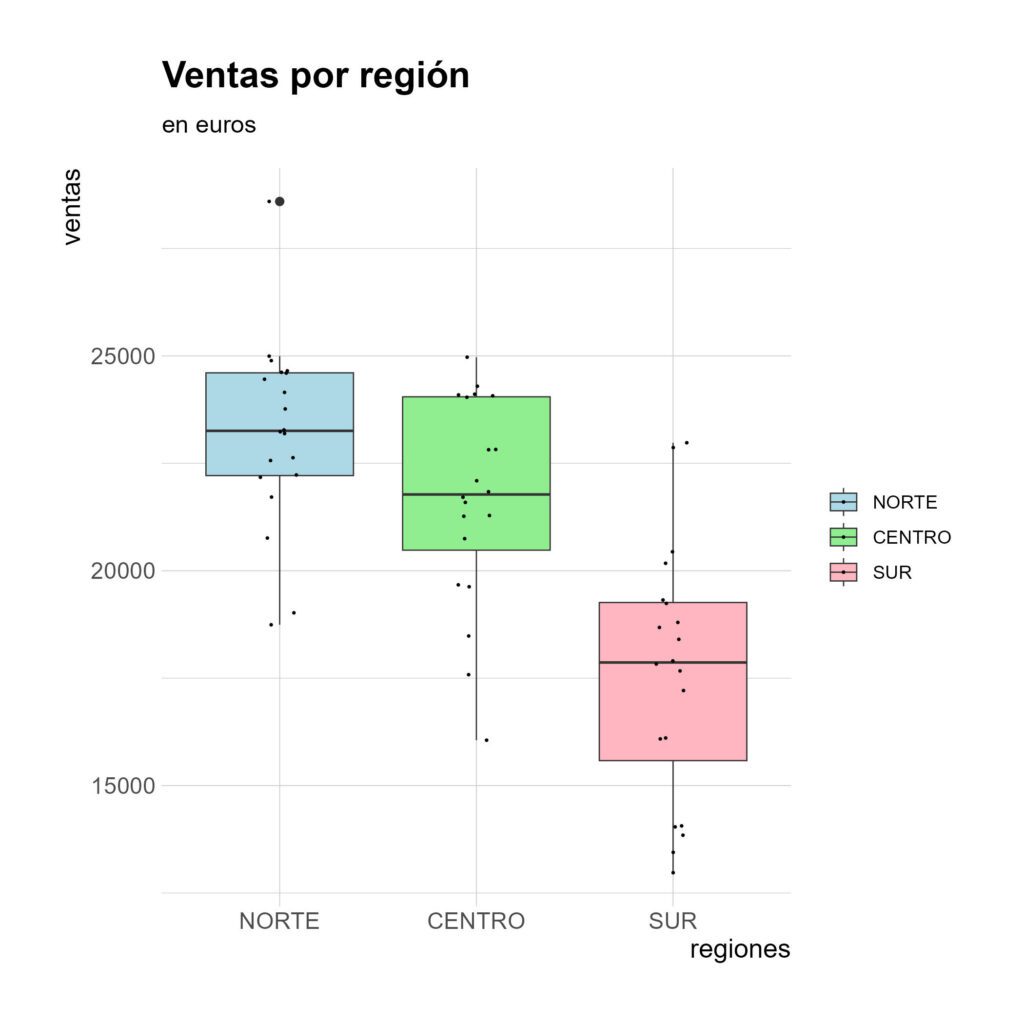
📦 ¿De dónde salen los datos en este supuesto práctico?

Para ilustrar este análisis sin depender de datos reales (que a menudo son confidenciales), he creado un conjunto de datos simulado, representativo de un escenario de ventas plausible.

Usamos la función rnorm() de R, que genera números aleatorios siguiendo una distribución normal (la típica “curva de campana”), ideal para simular fenómenos como ventas que fluctúan alrededor de un promedio.

🧠 ¿Qué significa esto?

• 20 observaciones por región, simulando ventas individuales (por ejemplo, por mes o por comercial).
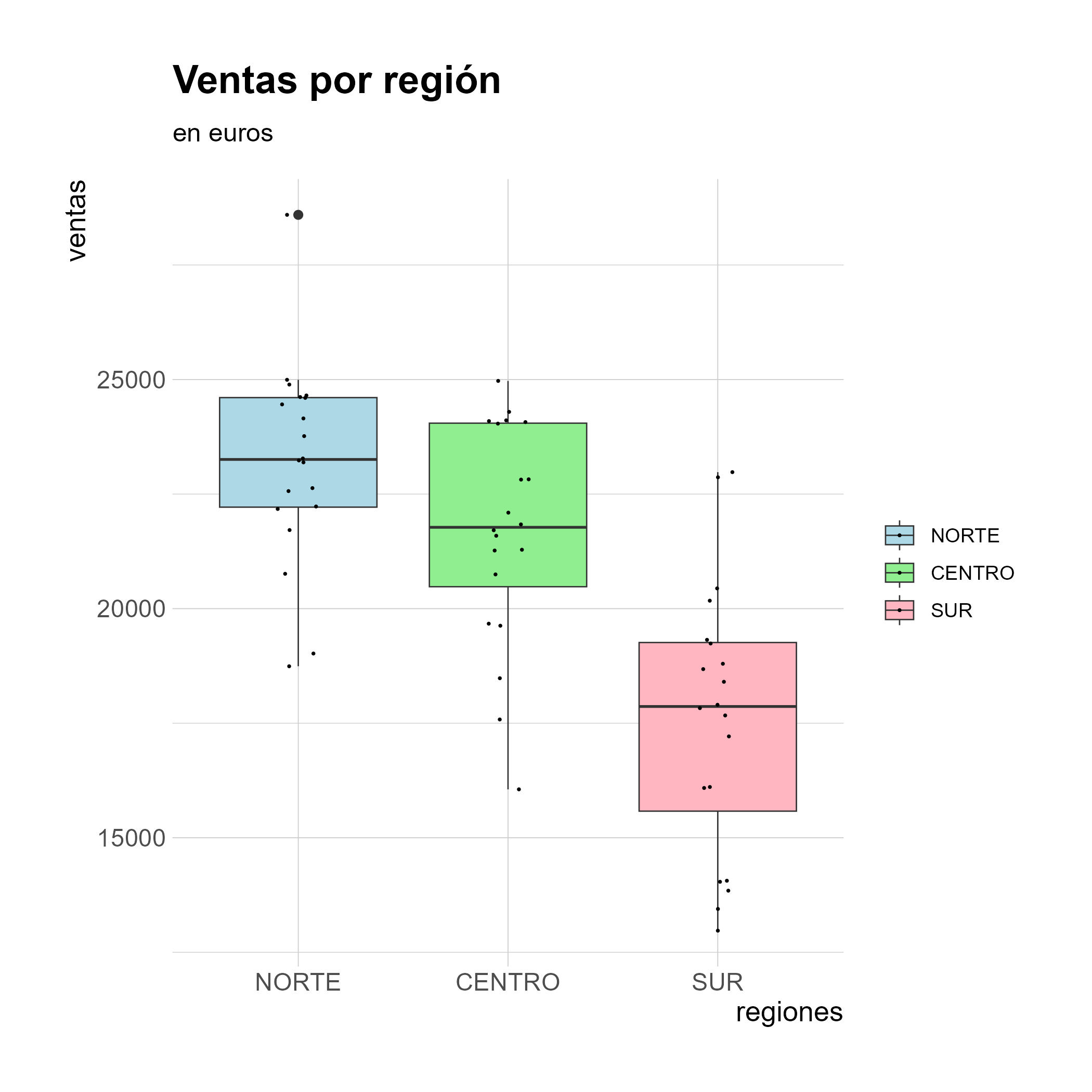
• Distintos promedios por zona, para reflejar escenarios de negocio realistas:
  • La zona norte tiene una media de ventas más alta.
  • La centro está cerca, pero ligeramente por debajo.
  • La sur muestra un rendimiento menor.

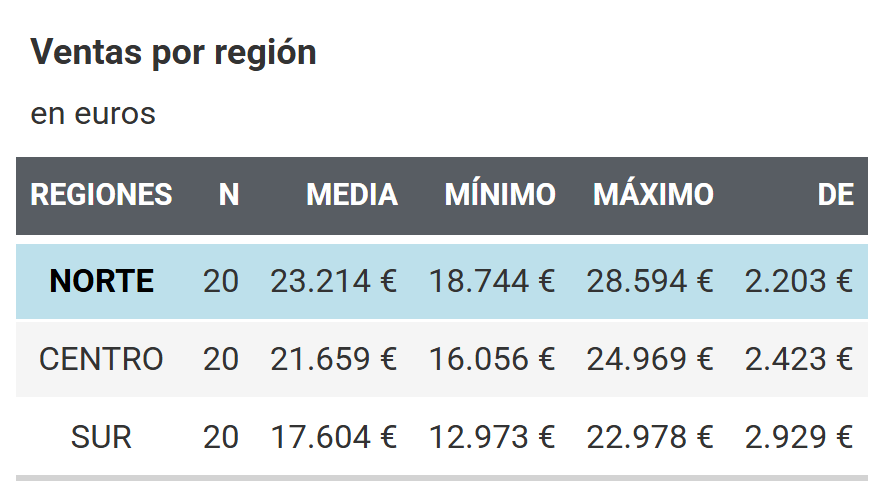
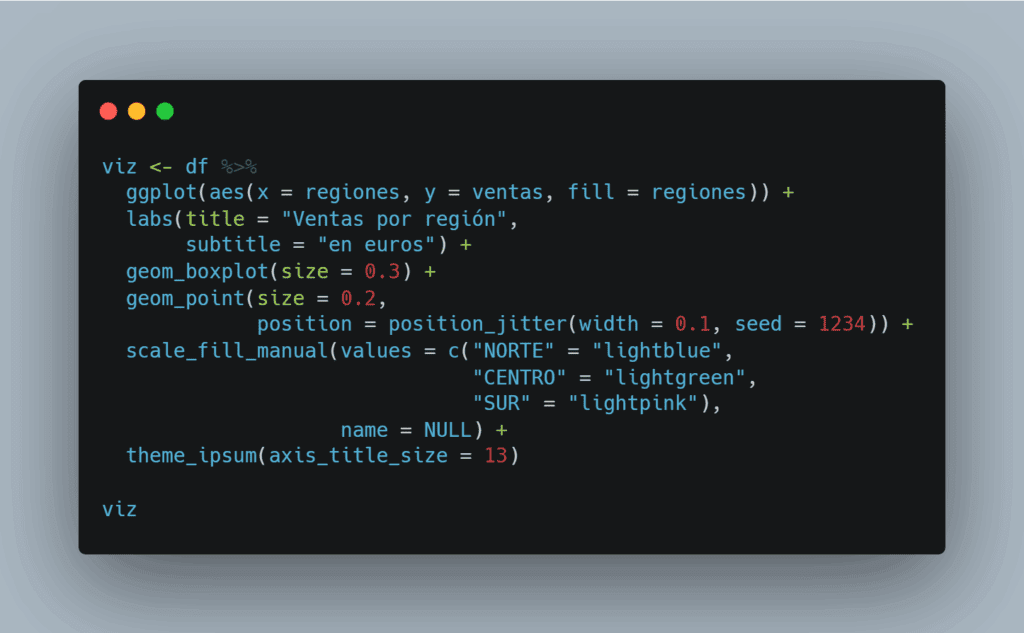
Representando gráficamente mediante boxplot.

Aplicamos un modelo ANOVA unifactorial, utilizando el siguiente código en R. Igualmente, validamos los supuestos de normalidad y homocedasticidad (explicación más abajo).

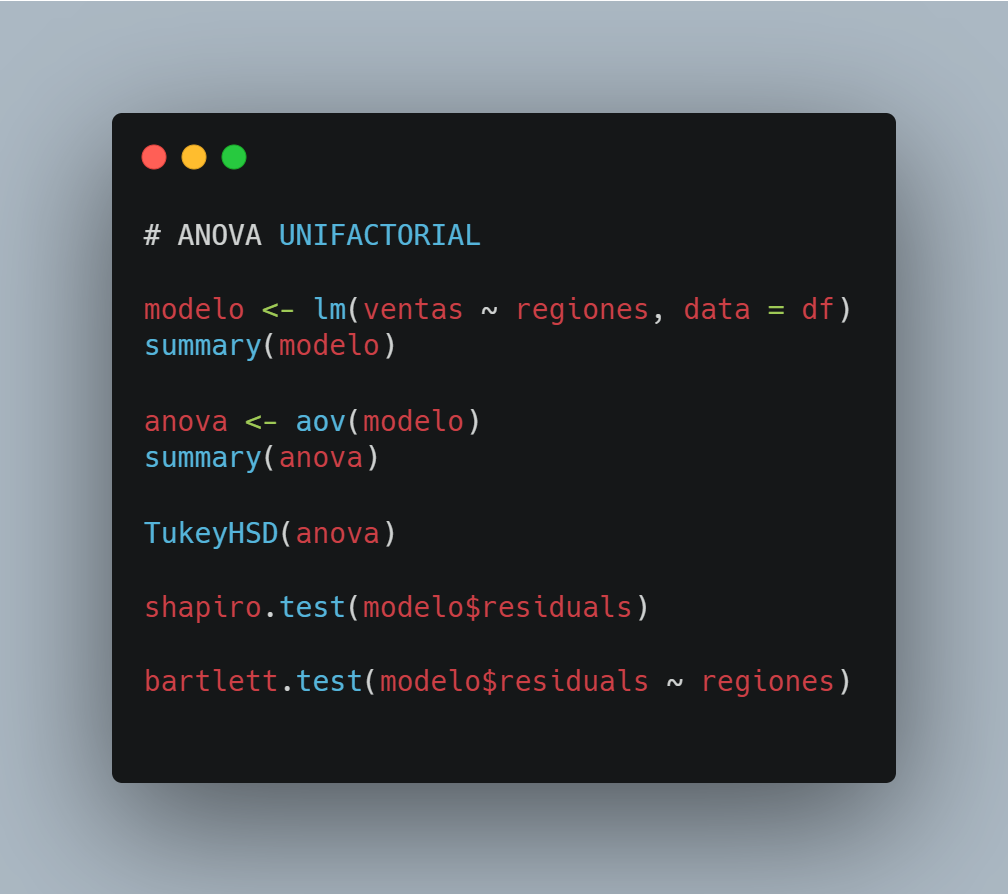
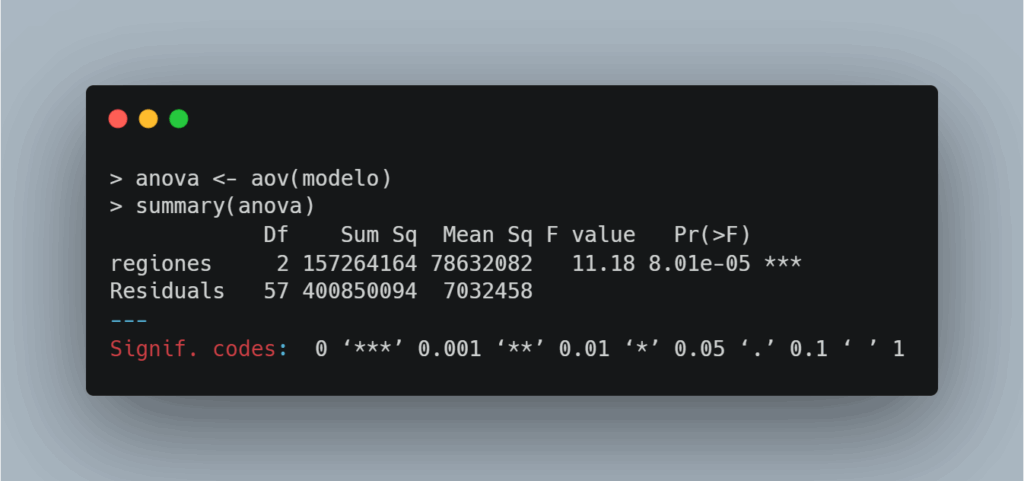
Esto nos permite evaluar si la región es un factor que influye de forma significativa en las ventas.

3. Interpretamos el valor p del ANOVA:
   • Si p < 0.05, podemos decir que existen diferencias significativas entre las regiones. En este caso, es así (se indica donde se ve Pr(>F), con valor 8.01 x 10^-5)
   • Si p ≥ 0.05, no hay evidencia estadística suficiente para afirmar que las ventas difieren por región.
4. Dado que encontramos diferencias significativas, aplicamos un test post-hoc de Tukey para ahondar más y saber qué regiones son distintas entre sí.

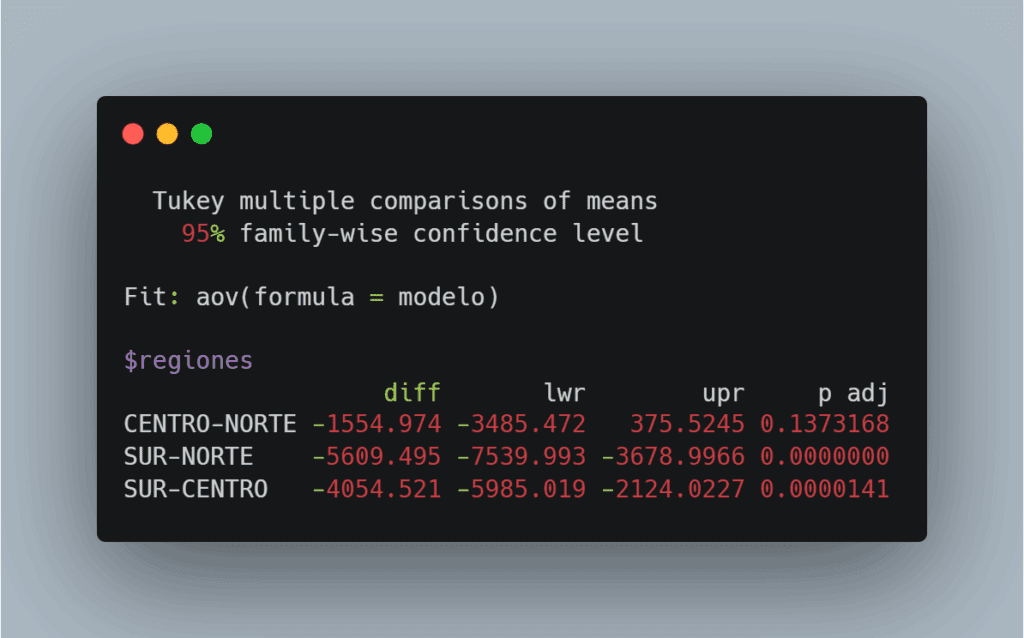
🧠 ¿Qué significa este resultado?

1. CENTRO vs NORTE
   • La diferencia media es de –1.555 € (parece que el centro vende menos).
   • El intervalo de confianza incluye el cero, por lo que la diferencia no es estadísticamente significativa.
   • p adj = 0.137 > 0.05 → no hay evidencia suficiente para afirmar que hay diferencia real entre centro y norte.
2. SUR vs NORTE
   • El sur vende de media 5.609 € menos que el norte.
   • El intervalo de confianza está completamente por debajo de 0.
   • p adj < 0.001 → la diferencia es altamente significativa.
   • ✅ Conclusión: El sur rinde significativamente peor que el norte.
3. SUR vs CENTRO
   • Diferencia de –4.055 € (el sur vende menos que el centro).
   • También significativa (p adj < 0.001).
   • ✅ Conclusión: El sur también rinde significativamente peor que el centro.

✅ Conclusión global

• Norte vs Centro: diferencias no significativas → podríamos considerar que rinden similarmente.
• Sur vs las otras regiones: diferencias significativas → el sur vende considerablemente menos que el norte y el centro.

🎯 ¿Qué se resuelve con este análisis?

• Identificar regiones con rendimientos anómalos (positivos o negativos).
• Tomar decisiones de negocio como:
  • redistribuir recursos comerciales,
  • ajustar objetivos por región,
  • replicar estrategias exitosas en zonas de bajo rendimiento.
• Ir más allá del “presentimiento” y trabajar con evidencia estadística objetiva.

Más información sobre los supuestos

🧪 Supuestos que se deben cumplir para utilizar ANOVA

Cuando usamos una técnica estadística como ANOVA para comparar medias entre grupos (por ejemplo, ventas entre regiones), no podemos aplicarla a ciegas. Esta técnica tiene ciertas condiciones que deben cumplirse para que sus resultados sean válidos.

Dos de las más importantes son:

1️⃣ Normalidad de los datos — Test de Shapiro-Wilk

Objetivo: Comprobar si los residuos del modelo ANOVA (es decir, las diferencias entre los valores observados y los promedios de cada grupo) siguen una distribución normal.

• Se aplica la prueba sobre los residuos del modelo, no sobre las variables originales.
• Hipótesis nula (H₀): Los residuos siguen una distribución normal.
• Hipótesis alternativa (H₁): Los residuos no siguen una distribución normal.

Interpretación:

Si el p-valor < 0.05, se rechaza H₀ → los residuos no son normales → el supuesto no se cumple.

Si el p-valor > 0.05, no se rechaza H₀ → los residuos pueden considerarse normales → el supuesto se cumple.

¿Qué hacemos si no se cumple? Podemos usar alternativas no paramétricas como el test de Kruskal-Wallis, que no requiere normalidad.

2️⃣ Igualdad de varianzas — Test de Bartlett

Objetivo: Verificar si los grupos del ANOVA tienen varianzas iguales (homocedasticidad).

• Se aplica a los grupos de la variable dependiente, no a los residuos.
• Hipótesis nula (H₀): Las varianzas entre los grupos son iguales.
• Hipótesis alternativa (H₁): Las varianzas son distintas.

Importante: Esta prueba asume normalidad, por eso primero se aplica Shapiro-Wilk para asegurarse de que esa condición se cumple.

Interpretación:

Si el p-valor < 0.05, se rechaza H₀ → hay desigualdad de varianzas → el supuesto se viola.

Si el p-valor > 0.05, no se rechaza H₀ → las varianzas son homogéneas → el supuesto se cumple.

¿Qué hacemos si no se cumple?
Si las varianzas son diferentes, podríamos:

• aplicar una versión robusta del ANOVA (como Welch’s ANOVA),
• -transformar los datos,
• o usar métodos no paramétricos.

Código utilizado en este caso práctico

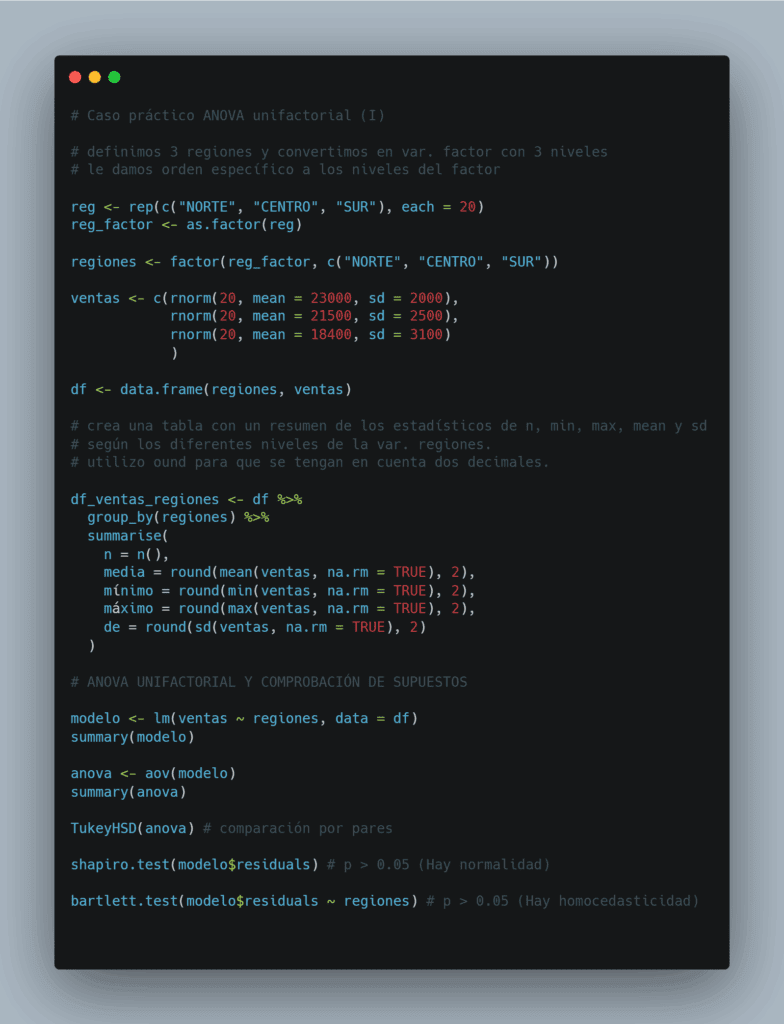
Código para el gráfico de boxplot