En este ejercicio aplicamos Análisis Discriminante Lineal (LDA) para distinguir especies de coleópteros morfológicamente muy similares entre sí, cuya identificación a simple vista resulta difícil o poco confiable. Aunque usamos datos simulados, la estructura del análisis es representativa de estudios reales en los que se busca caracterizar morfológicamente distintas especies animales.
Creamos un conjunto de datos con 5 especies del mismo género, cada una representada por 6 individuos.
Para cada individuo se midieron variables morfométricas clave:
- Longitud total del cuerpo (LT)
Desde el margen anterior del clípeo hasta el ápice del élitro. Es una medida básica que suele correlacionarse con el tamaño general del insecto. - Ancho máximo del pronoto (AP)
Es útil porque el pronoto (placa dorsal del tórax) varía mucho entre especies y puede tener valor diagnóstico. - Ancho máximo de los élitros (AE)
Los élitros (cobertores alares) son estructuras rígidas y bien conservadas morfológicamente, lo que los hace adecuados para comparación entre especies. - Índice cefálico (IC = ancho de la cabeza / largo de la cabeza)
Esta proporción puede reflejar diferencias sutiles en la forma de la cabeza, relevantes para separar especies crípticas. - Longitud de los élitros (LE)
Se mide desde la base (en el punto de articulación con el pronoto) hasta el ápice del élitro. Esta medida puede ser muy efectiva para diferenciar especies, especialmente aquellas con tamaños o formas alares diferentes.
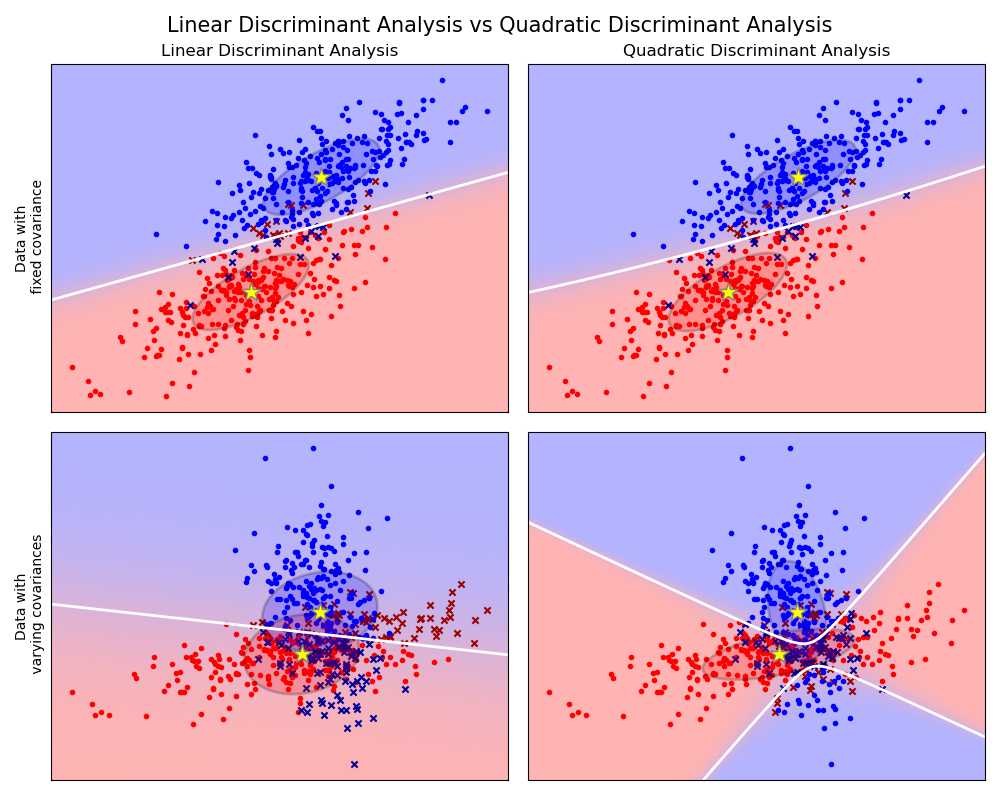
🧠 ¿Por qué usar LDA?
El Análisis Discriminante Lineal permite:
- Extraer combinaciones óptimas de variables morfológicas para separar grupos.
- Visualizar las diferencias entre especies en un espacio reducido (LD1 y LD2).
- Clasificar ejemplares nuevos con alta precisión en función de sus medidas.
- Detectar patrones morfológicos que no son evidentes en una inspección visual directa.
Cuando las especies objetivo son morfológicamente crípticas o muy similares, como puede en algunos casos, el LDA puede ser una herramienta útil para facilitar una identificación fiable.
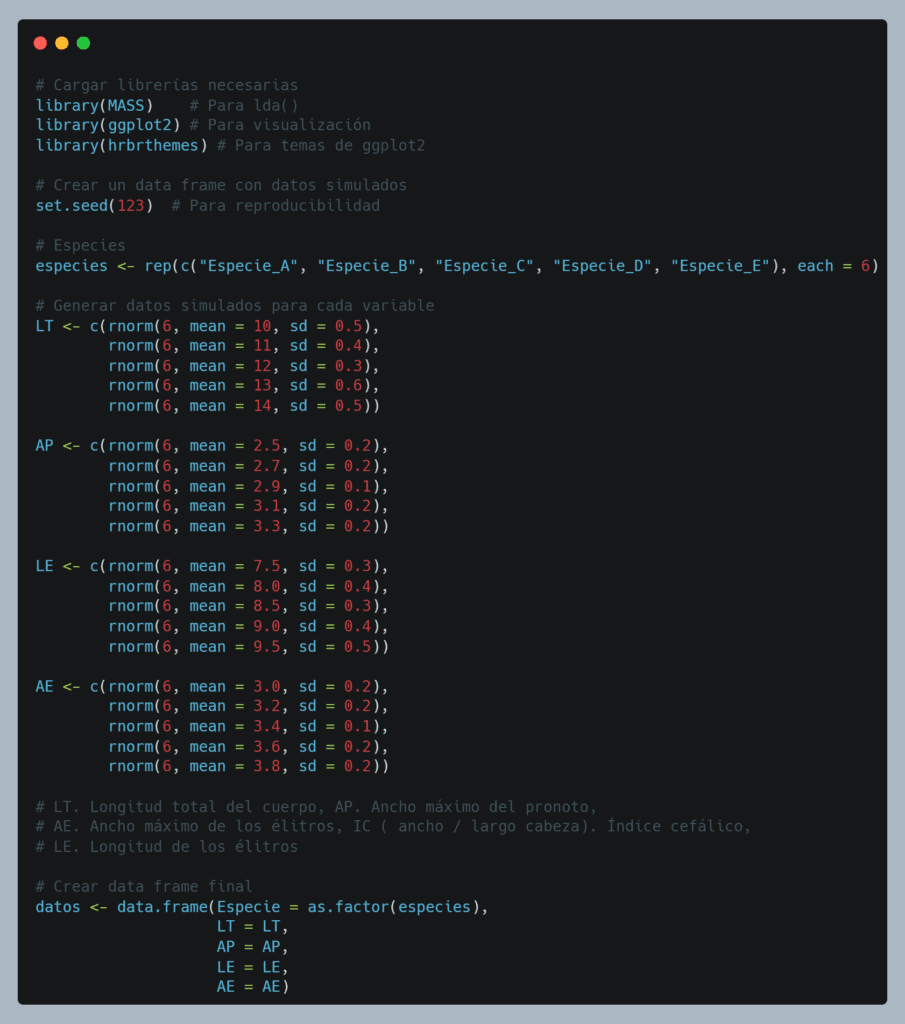
Este bloque de código construye el set de datos simulado con diferencias controladas entre especies, permitiendo que el análisis discriminante que vamos a realizar tenga una base clara sobre la cual trabajar. Es un paso fundamental tanto para fines didácticos como para ensayos previos a aplicar el método a datos reales. Las desviaciones estándar son similares, simulando una variabilidad comparable dentro de cada especie. Utilizamos rnorm() para generar datos aleatorios con distribución normal, imitando las medidas reales que podríamos obtener de coleópteros en campo o laboratorio.
Cada especie (A, B, C, D, E) recibe un conjunto de valores con medias diferentes por variable, lo que representa diferencias morfológicas esperadas entre especies.
Esto simula un caso donde las especies son morfológicamente parecidas, pero no idénticas, lo que reproduce el escenario buscado en esta práctica.
La diferencia de medias permite que, aunque los valores individuales se solapen, haya una separación estadística entre especies, lo cual es esencial para que LDA tenga sentido.
Con los datos ya preparados, ajustamos el modelo:

🔍 ¿Qué significa?
lda() es una función de la librería MASS que se utiliza para realizar un Análisis Discriminante Lineal.
El objetivo del LDA es encontrar combinaciones lineales de las variables explicativas que mejor separen los grupos definidos por la variable de clase (en este caso, la especie).
Especie ~ LT + AP + LE + AE indica que queremos predecir o clasificar la variable Especie usando como predictores morfométricos: LT (longitud total del cuerpo), AP (ancho del pronoto), LE (longitud de los élitros), AE (ancho de los élitros).
data = datos le dice a la función que busque esas variables dentro del data frame llamada datos, que contiene todas las observaciones simuladas.
Resultado obtenido:
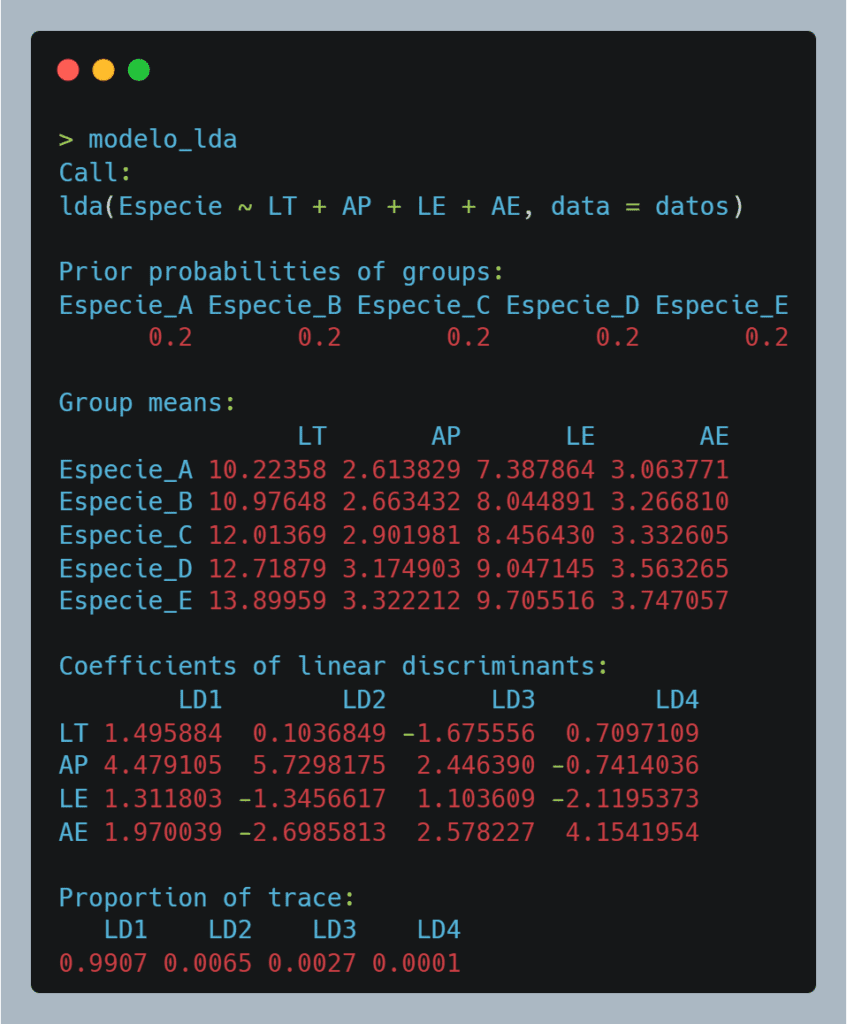
Explico en detalle los resultados:
(1) Probabilidad de los grupos. Como cada especie tiene 6 observaciones (30 en total), a priori, todas tienen la misma probabilidad 0.2 (20%).
(2) En «Group means» podemos ver las medias de las variables para cada una de las especies. El modelo va a utilizar estas diferencias en los promedios para aprender a separarlas. Como veis, hay una tendencia ascendente clara de la media de las variables entre especies, ideal para que LDA funcione bien (y como dijimos, es algo que se preparó desde el principio a la hora de generar los datos para la práctica).
(3) Los coeficientes de las funciones discriminantes. Cada columna representa una combinación lineal de las variables que maximiza la separación entre especies.
LD1 es la combinación más poderosa para separar las especies (99,07%). La fórmula sería así:
LD1 = 1.50×LT + 4.48×AP + 1.31×LE + 1.97×AE
Esto muestra que AP (ancho del pronoto) y AE (ancho de élitros) tienen un peso muy alto en la separación.
LD2, LD3 y LD4 son funciones secundarias que explican cada vez menos información.
Discriminante % de varianza explicada
LD1 99.07%
LD2 0.65%
LD3 0.27%
LD4 0.01%
LD1 domina completamente la separación de las especies (¡casi el 100%!). Las otras funciones son casi irrelevantes. En este caso, una sola dimensión (LD1) es suficiente para discriminar entre especies con gran precisión.
Ahora vamos a utilizar el modelo LDA ya entrenado (modelo_lda) para:
- Obtener las proyecciones de cada individuo en los nuevos ejes discriminantes (LD1, LD2, etc.).
- Guardar esas coordenadas en el
data framepara poder graficarlas y analizarlas.
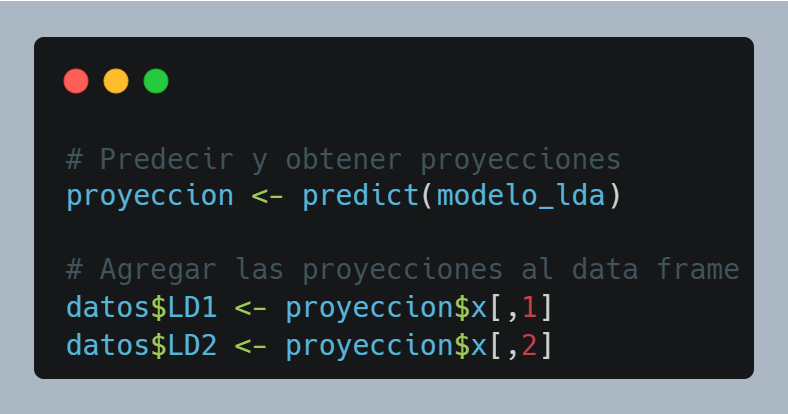
🔍 ¿Qué significa?
Esta función va a aplicar el modelo LDA a los mismos datos con los que fue entrenado, generando varias salidas (En otras entradas de este blog veremos como puede prepararse un grupo de datos para realizar el «training» del modelo y, los restantes, ser utilizados para el «testing». Ver más abajo).
class: la especie predicha para cada individuo (útil si estuviéramos clasificando nuevos datos).
posterior: las probabilidades de pertenencia a cada clase (especie).
x: las coordenadas de cada individuo proyectadas en las funciones discriminantes (LD1, LD2, etc.).
Aquí nos interesa x, que es una matriz con tantas filas como individuos, y columnas como funciones discriminantes generó el modelo (en este caso, 4 especies → 3 discriminantes, pero normalmente usamos las dos primeras: LD1 y LD2).
Una vez realizado, podemos hacer un gráfico para ver el resultado.
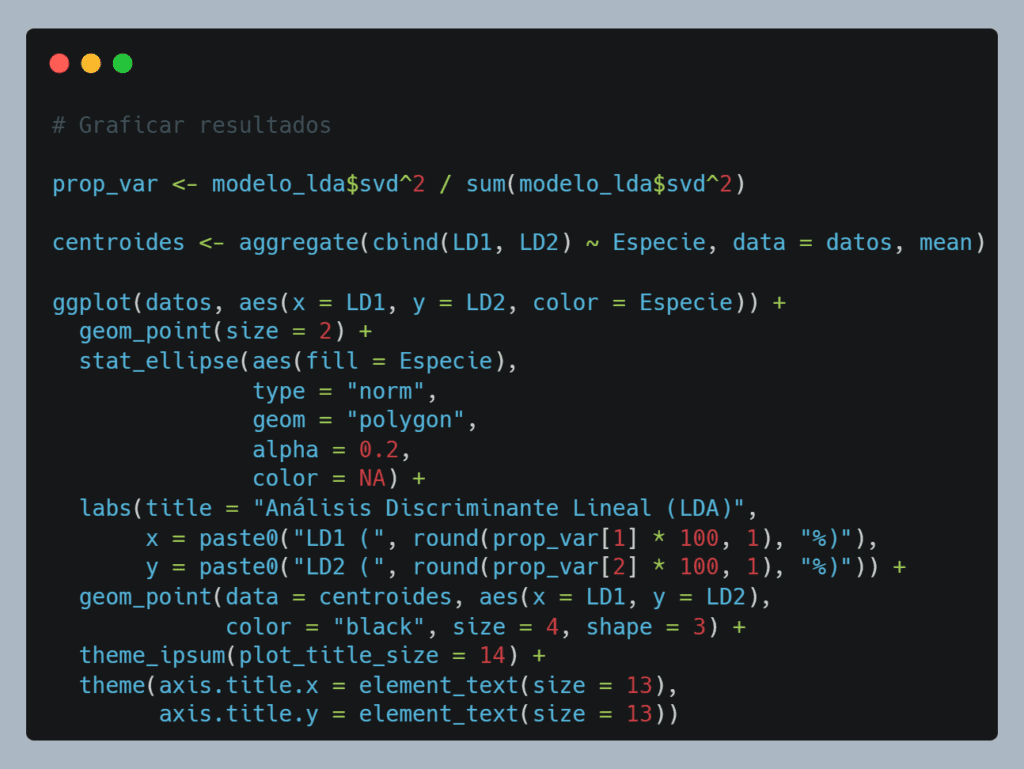
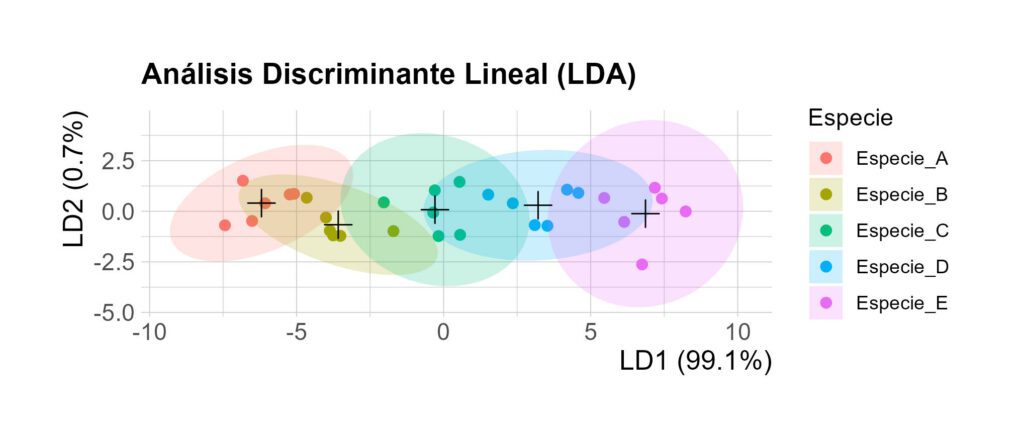
🎯 ¿Qué representa el gráfico de LD1 vs LD2? El gráfico muestra la proyección de cada observación (individuo de cada especie de escarabajo estudiado) en un nuevo espacio definido por las funciones discriminantes encontradas por el modelo LDA:
LD1 (eje horizontal): la que resultó ser la combinación lineal más importante para separar las especies.
LD2 (eje vertical): la segunda combinación más importante, aunque en este caso práctico solo explica un 0.65% de la varianza, así que aporta poco.
–
📈 Interpretación visual de estos resultados
Cada punto se corresponde con una observación individual (un escarabajo). La posición del punto se basa en sus valores proyectados sobre LD1 y LD2. El color indica a qué especie realmente pertenece (según datos$Especie).
Agrupamiento de puntos. Si el modelo funciona bien, los puntos de la misma especie formarán grupos separados, como vemos que ha ocurrido en este caso. Mientras más distantes hayan quedado los grupos entre sí, mejor está discriminando el modelo.
Separación a lo largo de LD1. Como LD1 explica el 99% de la varianza, es el eje más importante. Según esto, la mayoría de la discriminación entre especies ocurre de izquierda a derecha (LD1). Por otro lado, LD2 apenas contribuye a la separación (solo 0.6%), aunque puede mostrar pequeños matices.
–
📊 Predicción con nuevos valores
Imaginemos que ahora tenemos las medidas de un nuevo individuo capturado, y queremos identificar su especie atendiendo al modelo discriminante que hemos creado:
Las medidas serían las siguientes:
LT = 12.4
AP = 2.85
LE = 8.6
AE = 3.5
Podríamos predecir la especie con este código:

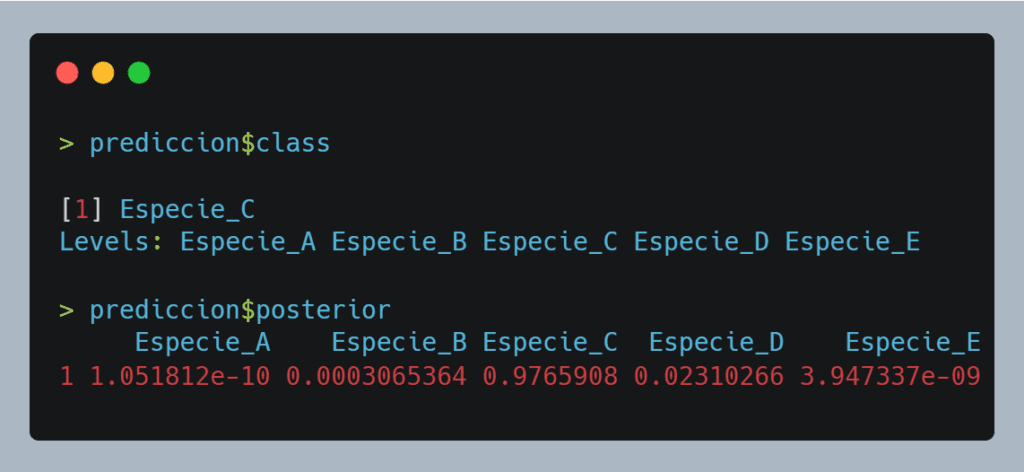
Los resultados muestran que las medidas nos llevarían a la ESPECIE_C y que la probabilidad de pertenencia a esa clase sería del 0.9765908 (muy cercana a 1).
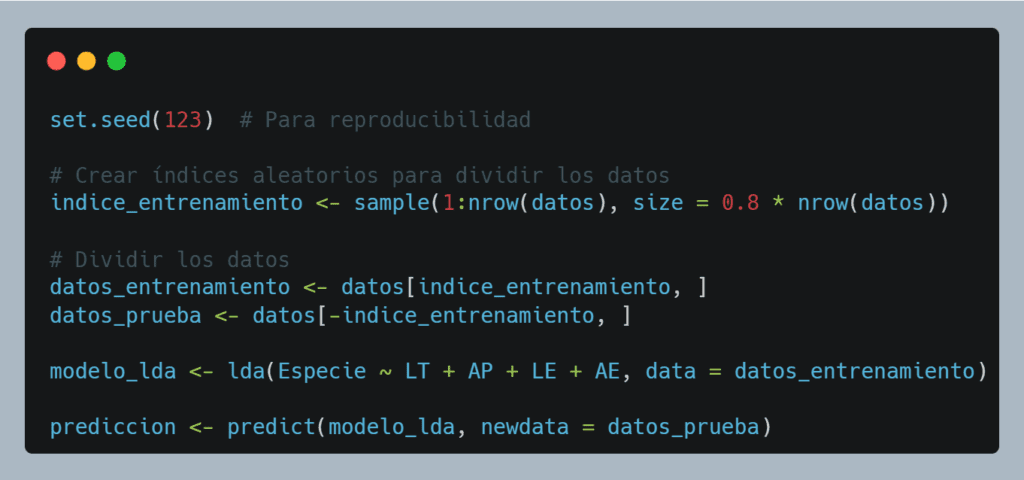
ANEXO: TRAINING y TESTING
🎯 ¿Por qué dividir en training y testing?
Dividir los datos en conjuntos de entrenamiento (training) y prueba (testing) es una práctica fundamental cuando queremos evaluar objetivamente el rendimiento de un modelo predictivo, como el LDA en este caso. Cuando entrenas y evalúas un modelo con los mismos datos, puedes obtener un resultado demasiado optimista. Es decir, el modelo puede parecer muy preciso, pero tienes que tener en cuenta que en realidad ha “memorizado” los datos, y no necesariamente funcionará bien con individuos nuevos.
Por eso dividimos los datos así:
Conjunto de prueba (testing set):
Se usa después, para evaluar qué tan bien el modelo puede clasificar nuevos individuos.
Conjunto de entrenamiento (training set):
Se usa para ajustar (entrenar) el modelo.
Con esto conseguimos:
- Evaluar la capacidad de generalización del modelo.
- Evitar sobreajuste (overfitting) al no validar con los mismos datos que se usaron para entrenar.
- Obtener métricas realistas sobre el desempeño del modelo en datos nuevos.
Aunque esto lo veremos en más detalle en próximas entradas, un ejemplo de codigo en R para realizar esto podría ser: