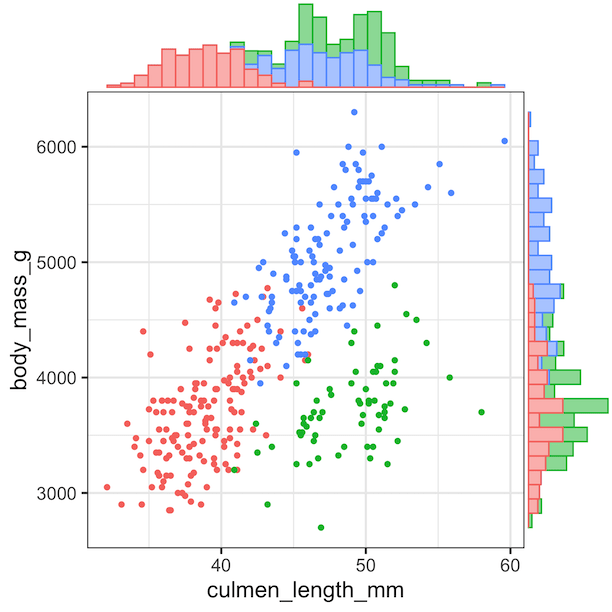
Los gráficos marginales permiten visualizar simultáneamente la relación entre dos variables y la distribución individual de cada una. Esto es especialmente útil porque:
Pueden ayudar a detectar patrones y anomalías: Mientras el scatterplot muestra cómo se relacionan las variables, los gráficos marginales ofrecen más información y pueden revelar si alguna variable está sesgada, tiene múltiples picos (multimodal), o contiene valores atípicos.
- Contextualizar la correlación: A veces, dos variables pueden parecer relacionadas, pero sus distribuciones pueden indicar heterogeneidad o agrupamientos que un scatterplot solo no mostraría.
- Facilitar la interpretación: Al ver las distribuciones marginales, los analistas pueden entender mejor el rango y concentración de datos, mejorando la toma de decisiones basada en los gráficos.
- Presentación profesional: No hay que desdeñar el hecho de que añadir gráficos marginales en reportes o presentaciones aporta claridad visual y un toque de sofisticación que puede ser muy valorado en entornos académicos o empresariales.
Librerías que vamos a utilizar en este ejemplo.
Creamos un dataset con dos 200 valores para cada variable, x e y. Para ello, utilizamos la función rnorm de R (con el fin de generar números aleatorios que siguen una distribución normal — también conocida como distribución gaussiana o de campana–). Tras esto, con data.frame generamos la tabla de datos.

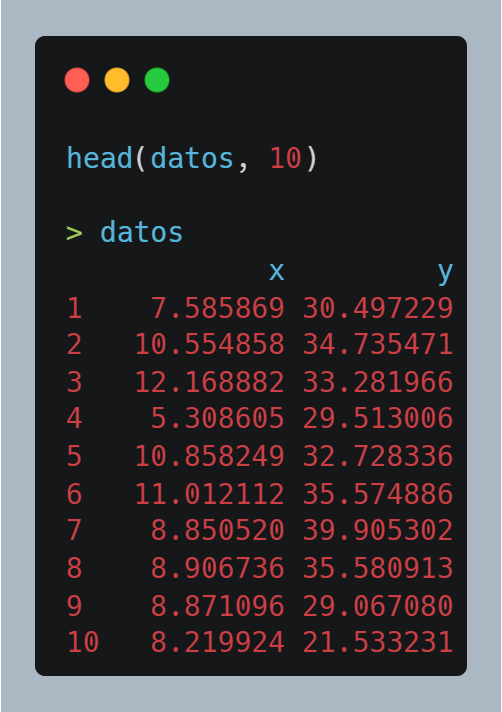
Para que veáis la estructura de datos, con head(datos, 10) podemos ver las 10 primeras observaciones del data frame que acabamos de crear.
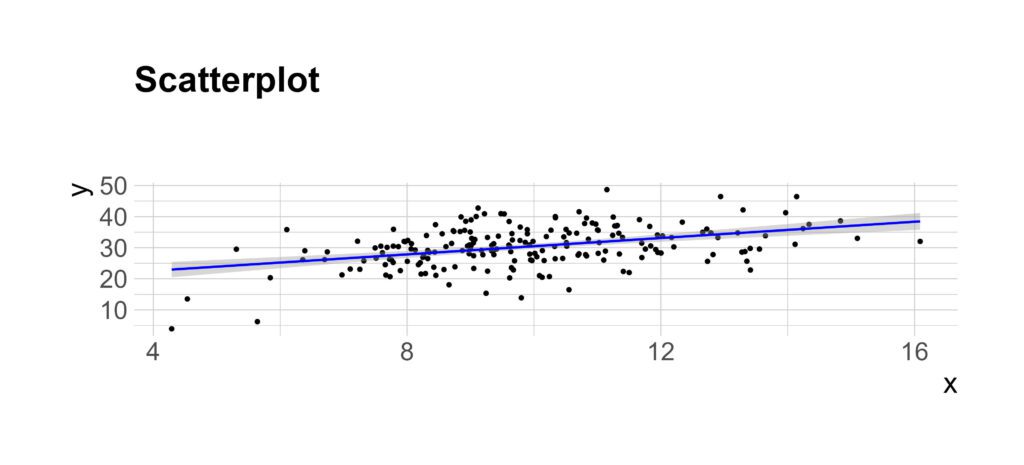
Ahora creamos el gráfico de dispersión (scatterplot) con el siguiente código, y lo mostramos. He añadido geom_smooth(method = «lm») para mostrar también la línea de tendencia.

Ahora usamos la función ggMarginal del paquete ggExtras para añadir al gráfico el densigrama «en este caso». Existe la posibilidad de añadir otros tipos de gráficos marginales, como un histograma, boxplot, gráficos de violín etc.
El gráfico resultante sería el siguiente:
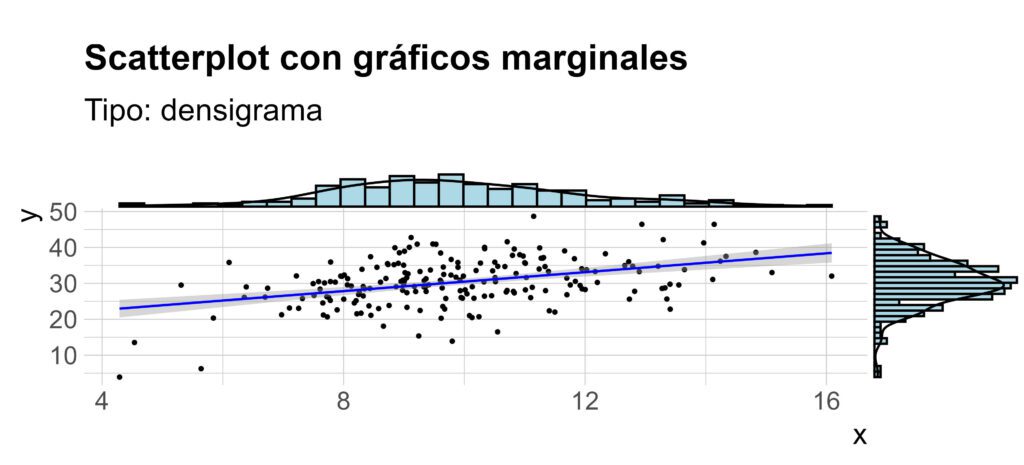
✏️ Relación entre X e Y (gráfico de dispersión / scatterplot)
La variable x sigue una distribución normal centrada en 10 con una dispersión moderada (sd = standard deviation = 2).
La variable y es generada con media 20, sd 6 y, posteriormente, sumando + x. Por lo tanto, y está correlacionada positivamente con x, pero con bastante variabilidad vertical (por el ruido de sd = 6).
Así, a medida que x aumenta, y también tiende a aumentar. Pero para un mismo valor de x, y puede tener un rango bastante amplio. Esto se observa gráficamente como una nube de puntos inclinada positivamente, pero dispersa.
–
✏️ Comentario sobre los gráficos marginales
🟢 Distribución marginal de x (arriba)
Tiene forma normal (simétrica) centrada cerca de 10, con un ligero aplanamiento típico de una muestra de tamaño 200. La curva es relativamente estrecha, reflejando la baja dispersión (sd = 2). Visualmente se ve una campana bien definida y concentrada.
🟢 Distribución marginal de y (a la derecha)
Aunque y está influida por una distribución normal (media 20, sd 6), al sumar x (media 10), su distribución se desplaza hacia valores más altos. En la práctica, y queda centrada aproximadamente alrededor de 30.
La curva es más ancha y más aplanada, ya que la desviación estándar combinada es considerable.
Puedes ver una mayor dispersión horizontal: la densidad se reparte en un rango más amplio que x.
–
✏️ Interpretación general
El gráfico completo (dispersión + márgenes) muestra cómo x y y están positivamente relacionados, pero con bastante variabilidad.
Los gráficos marginales ayudan a entender:
Que x está mucho más concentrado (menos disperso).
Que y es más difuso, con valores más alejados de la media.