La normalidad en los datos actúa como una base fundamental para el análisis estadístico riguroso bajo el prisma de un buen número de técnicas estadísticas. La existencia de normalidad en los datos asegura que las pruebas y técnicas estadísticas aplicadas sean realmente válidas y confiables, permitiendo así la toma de decisiones informadas. La ausencia de normalidad puede comprometer la integridad de los resultados y conducir a interpretaciones erróneas, por lo que la verificación de este atributo se convierte en un paso crítico, incluso, en la preparación previa de los datos para su análisis.
A medida que nos adentramos en los entresijos de la normalidad, se vuelve claro que la idoneidad de ciertas técnicas estadísticas depende en gran medida de su presencia. Desde la prueba t (t-student) hasta el análisis de varianza (ANOVA) y más allá, estas herramientas requieren que los datos sigan una distribución normal para generar resultados significativos y confiables. Sin embargo, es importante tener en cuenta que, en ocasiones, los conjuntos de datos pueden desviarse de la normalidad, lo que plantea desafíos adicionales y la necesidad de utilizar métodos alternativos para obtener conclusiones estadísticamente sólidas.
Para evaluar la normalidad, los profesionales recurren a diversas pruebas, como la prueba de Kolmogórov-Smirnov, la prueba de Shapiro-Wilk y la prueba de Lilliefors, entre otras. Estas pruebas permiten determinar si los datos se ajustan a una distribución normal o si se desvían significativamente de ella, lo que proporciona una comprensión más clara de la viabilidad de aplicar ciertas técnicas estadísticas. De la misma forma, es posible utilizar gráficas que permiten realizar un estudio visual de la distribución de nuestros datos.
Aquí tenéis los enlaces a la publicación del documento de prácticas en RPubs y GitHUb. Los tests y gráficos de esta práctica se han realizado en el lenguaje de programación R. Consultar los documentos RMarkdown, y el .pdf para ver los ejemplos realizados y las explicaciones sobre los procedimientos.
Empezamos…
Distribución normal
La distribución normal, también conocida como gaussiana, es una de las distribuciones más importantes en estadística y se caracteriza por su forma de campana y propiedades matemáticas bien definidas.
- Forma de campana: La distribución normal tiene una forma de campana simétrica alrededor de su media. A agruparse la mayoría de los valores alrededor de la media, la mediana y la moda son aproximadamente iguales.
- Simetría: La distribución normal es simétrica alrededor de su media. Esto indica que las colas de la distribución se extienden hacia los valores positivos y negativos de manera similar, lo que implica que hay igual probabilidad de observar valores por encima y por debajo de la media.
- Parámetros específicos: Una distribución normal está completamente definida por su media y su desviación estándar. La media determina el centro de la distribución y la desviación estándar determina la dispersión de los datos alrededor de la media.
- Regla empírica: La distribución normal sigue la regla empírica, que establece que alrededor del 68% de los datos se encuentran dentro de una desviación estándar de la media, alrededor del 95% dentro de dos desviaciones estándar y casi el 99.7% dentro de tres desviaciones estándar.
- Función de densidad de probabilidad específica: La función de densidad de probabilidad de una distribución normal está definida matemáticamente por la ecuación de la campana de Gauss.
Tests de Normalidad
Las pruebas de normalidad en estadística son métodos utilizados para determinar si un conjunto de datos se distribuye normalmente o no.
La verificación de la normalidad de los datos es fundamental en muchos análisis estadísticos y pruebas de hipótesis. Algunos de los métodos comunes para probar la normalidad incluyen:
- Prueba de Kolmogorov-Smirnov: Esta prueba compara la distribución de los datos con una distribución normal teórica. Evalúa si la muestra tiene la misma distribución que una distribución normal específica.Esta prueba es útil cuando se tienen muestras grandes (n > 50) y no se dispone de información previa sobre la distribución de los datos.
- Prueba de Shapiro-Wilk: Esta prueba también se utiliza para evaluar si una muestra proviene de una población con distribución normal. Esta prueba es más adecuada para muestras pequeñas (n < 50) y es sensible a la detección de desviaciones de la normalidad en las colas de la distribución.
- Prueba de Lilliefors: Similar a la prueba de Kolmogorov-Smirnov, pero se recomienda especialmente para tamaños de muestra pequeños debido a sus ajustes para tamaños de muestra más reducidos.
- Prueba de Jarque-Bera: Esta prueba se utiliza para evaluar la normalidad basándose en la asimetría y la curtosis de los datos. Es útil cuando se sospecha que los datos pueden no seguir una distribución normal debido a desviaciones en estos dos parámetros.
- Prueba de Anderson-Darling: Esta prueba es una medida de la bondad de ajuste de un conjunto de datos a una distribución particular, como la distribución normal.Esta prueba es útil cuando se busca una evaluación detallada de la bondad de ajuste de los datos a una distribución normal. Es más efectiva en la detección de desviaciones en las colas de la distribución.
Es importante recordar que ninguna de estas pruebas puede demostrar con certeza que un conjunto de datos proviene de una distribución normal. En lugar de eso,…
- estas pruebas proporcionan una indicación de la probabilidad de que los datos puedan provenir de una distribución normal.
- Además, es crucial considerar el tamaño de la muestra.
Dataset Iris
iris es un conjunto de datos incorporado en el entorno de R de forma predeterminada. Este contiene información sobre diferentes medidas de las flores de 3 especies del género iris (Iris setosa, I. versicolor, e I. virginica), como la longitud y el ancho de los pétalos y sépalos. Estos datos son muy utilizados en la enseñanza y práctica de análisis estadístico y aprendizaje automático en R.
Iris cuenta con 150 observaciones, para 5 variables y las 3 especies de Iris. Cada una de estas especies tiene 50 observaciones.
str(iris)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...head(iris, 10)| Sepal.Length<dbl> | Sepal.Width<dbl> | Petal.Length<dbl> | Petal.Width<dbl> | Species<fct> | |
|---|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 | setosa |
| 7 | 4.6 | 3.4 | 1.4 | 0.3 | setosa |
| 8 | 5.0 | 3.4 | 1.5 | 0.2 | setosa |
| 9 | 4.4 | 2.9 | 1.4 | 0.2 | setosa |
| 10 | 4.9 | 3.1 | 1.5 | 0.1 | setosa |
1-10 of 10 rows
unique(iris$Species)## [1] setosa versicolor virginica
## Levels: setosa versicolor virginica# 50 observaciones para cada especie, por ejemplo:
sum(iris$Species == "setosa")## [1] 50Gráficos para el análisis
Histogramas
Nos vamos a fijar ahora en las medidas de la longitud de los pétalos y sépalos, sin diferenciar entre las especies, y vamos a representar gráficamente los histogramas de estas medidas. Observando gráficamente los datos podemos hacernos una idea de si estos se distribuirían de forma normal o, por el contrario, se alejan de esta distribución.
hist(iris$Petal.Length,
prob = TRUE,
main = "Histograma Pétalos Iris",
sub = "dataset: Iris | Edgar Anderson's Iris Data",
xlab = "Longitud (mm)",
ylab = "Frecuencia",
cex.lab = 1.2,
cex.axis = 1,
mgp = c(2.4, 1, 0),
col = "#F2F4F4")
lines(density(iris$Petal.Length), lwd = 2, col = '#C39BD3')
x <- seq(min(iris$Petal.Length), max(iris$Petal.Length), length = 40)
f <- dnorm(x, mean = mean(iris$Petal.Length), sd = sd(iris$Petal.Length))
lines(x, f, col = "#6C3483", lwd = 2) # Normal
abline(v=median(iris$Petal.Length), col="blue")
abline(v=mean(iris$Petal.Length), col="green")
legend("topright", legend = "Densidad", col = "#C39BD3",
lty = 1, lwd = 2, bty = "n", cex = 0.9)
legend("topright", legend = "Normal", col = "#6C3483",
lty = 1, lwd = 2, bty = "n", cex = 0.9, inset = c(0, -0.1), xpd = TRUE)
legend("topright", legend = "Media", col = "green",
lty = 1, lwd = 2, bty = "n", cex = 0.9, inset = c(0, 0.1), xpd = TRUE)
legend("topright", legend = "Mediana", col = "blue",
lty = 1, lwd = 2, bty = "n", cex = 0.9, inset = c(0, 0.2), xpd = TRUE)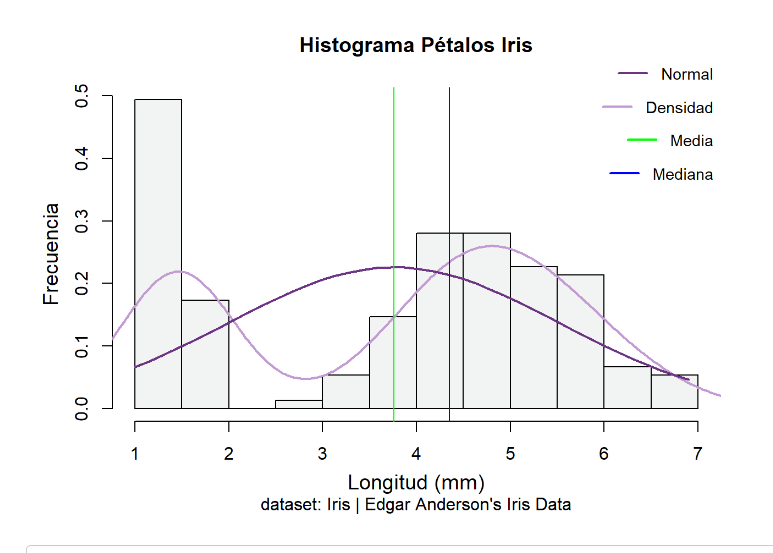
hist(iris$Sepal.Length,
prob = TRUE,
main = "Histograma Sépalos Iris",
sub = "dataset: Iris | Edgar Anderson's Iris Data",
xlab = "Longitud (mm)",
ylab = "Frecuencia",
cex.lab = 1.2,
cex.axis = 1,
ylim = c(0, 0.50),
mgp = c(2.4, 1, 0),
col = "#F2F4F4")
lines(density(iris$Sepal.Length), lwd = 2, col = '#C39BD3')
x <- seq(min(iris$Sepal.Length), max(iris$Sepal.Length), length = 40)
f <- dnorm(x, mean = mean(iris$Sepal.Length), sd = sd(iris$Sepal.Length))
lines(x, f, col = "#6C3483", lwd = 2) # Normal
abline(v=median(iris$Sepal.Length), col="blue")
abline(v=mean(iris$Sepal.Length), col="green")
legend("topright", legend = "Densidad", col = "#C39BD3",
lty = 1, lwd = 2, bty = "n", cex = 0.9)
legend("topright", legend = "Normal", col = "#6C3483",
lty = 1, lwd = 2, bty = "n", cex = 0.9, inset = c(0, -0.1), xpd = TRUE)
legend("topright", legend = "Media", col = "green",
lty = 1, lwd = 2, bty = "n", cex = 0.9, inset = c(0, 0.1), xpd = TRUE)
legend("topright", legend = "Mediana", col = "blue",
lty = 1, lwd = 2, bty = "n", cex = 0.9, inset = c(0, 0.2), xpd = TRUE)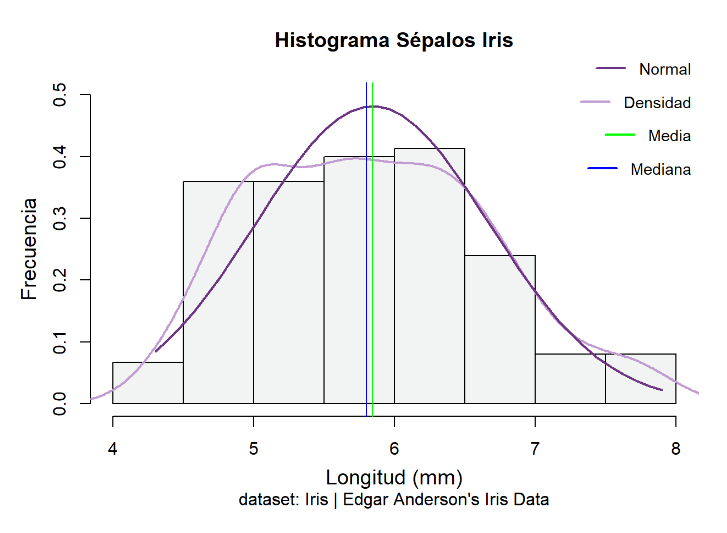
Diagrama QQ
Un diagrama QQ (quantile-quantile) es una representación gráfica que se utiliza para comparar la distribución de probabilidades de dos conjuntos de datos. En el eje horizontal se representan los cuantiles teóricos esperados de una distribución específica (generalmente la distribución normal), mientras que en el eje vertical se representan los cuantiles observados de los datos reales que se están analizando.
Al comparar la distribución teórica con la distribución real de los datos en el gráfico, se puede determinar si ambas distribuciones siguen un patrón similar. Si los puntos en el gráfico caen aproximadamente a lo largo de una línea diagonal, esto sugiere que los datos siguen la distribución teórica asumida. Por otro lado, si los puntos se desvían significativamente de la línea diagonal, indica que los datos no se ajustan bien a la distribución teórica asumida.
En este caso, el gráfico muestra que los datos de longitud de los pétalos de las especies del Gen. Iris analizadas, no siguen una distribución normal.
qqnorm(iris$Petal.Length,
main = "Gráfico Q-Q Longitud de los pétalos",
sub = "Analizando la normalidad de los datos",
xlab = "Cuantiles de los datos teóricos",
ylab = "Cuantiles de los datos observados (muestra)",
cex.lab = 1.2,
cex.axis = 1,
mgp = c(2.4, 1, 0),
col = "#2ECC71")
qqline(iris$Petal.Length,
col = "#2874A6",
lty = 2,
lwd = 1)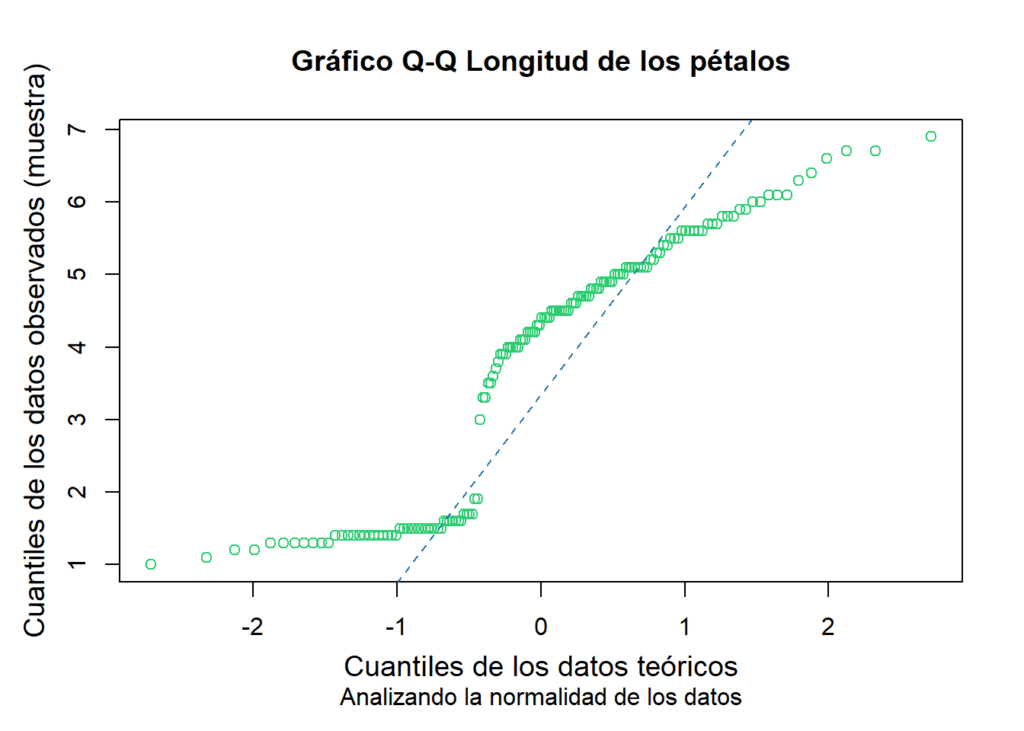
En este otro caso, la longitud de los sépalos de las tres especies de Iris estudiadas presentan una distribución que se ajusta a la normal, o gaussiana.
qqnorm(iris$Sepal.Length,
main = "Gráfico Q-Q",
sub = "Analizando la normalidad de los datos",
xlab = "Cuantiles de los datos teóricos",
ylab = "Cuantiles de los datos observados (muestra)",
cex.lab = 1.2,
cex.axis = 1,
mgp = c(2.4, 1, 0),
col = "#2ECC71")
qqline(iris$Sepal.Length,
col = "#2874A6",
lty = 1,
lwd = 1)
También podemos realizar este otro gráfico con la función qqPlot de la librería car. Con esta función podemos mostrar el intervalo de confianza del 95%, lo que indicaría que el gráfico Q-Q muestra un envelope alrededor de la línea diagonal que cubre el 95% de los puntos si los datos se ajustan a la distribución teórica especificada (normal en este caso, indicado en distribution = “norm”).
Con la función qqPlot de cars es posible indicar con qué distribución comparamos el ajuste de los datos y, que se muestre el intervalo de confianza que indiquemos. Es posible, por ejemplo, calcularlo para un 99%, en vez del 95%.
qqPlot(iris$Sepal.Length,
distribution = "norm",
main = "Gráfico Q-Q",
xlab = "Cuantiles teóricos",
ylab = "Cuantiles observados (muestra)",
envelope = 0.95, col=carPalette()[1], col.lines = carPalette()[5],
line=c("quartiles", "robust", "none"),
id = FALSE, grid = TRUE,
pch = 19,
cex = 0.8,
lwd = 1)
# si quieres puedes poner encima la línea media con qqline
qqline(iris$Sepal.Length,
col = "#CB4335",
lty = 1,
lwd = 1)
Tests de normalidad
Kolmogorov-Smirnov
Vamos a calcular el test de KS a las variables longitud de los pétalos y sépalos de las especies del Gen. Iris. El número de observaciones es de 150 (condición necesaria para que pueda realizarse este test (n > 50)).
En el caso de la longitud de los pétalos, la función ks.test (de base en R), está utilizando la distribución normal teórica (pnorm) con la media y la desviación estándar de la variable mpg en el conjunto de datos mtcars como parámetros. El valor de D es 0.19815 y, el valor p es 1.532e-05 (muy pequeño). Ho de normalidad rechazada. El p valor está por debajo de 0.06, por lo que hay evidencia significativa para rechazar la hipótesis nula de que los datos de Petal.Length siguen una distribución normal. Ho rechazada. Haciendo el histograma de la variable podemos también descartar que la distribución de la longitud de los pétalos sea normal, al tener las observaciones una distribución alejada de la típica forma de campana de Gauss.
Por otro lado, ocurre lo contrario para la longitud de los sépalos, con un p-valor de 0.1891, no se puede rechazar la Ho y se concluye que los datos si tienen una distribución normal.
length(iris$Petal.Length)## [1] 150ks.test(iris$Petal.Length, "pnorm",
mean = mean(iris$Petal.Length),
sd = sd(iris$Petal.Length))##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: iris$Petal.Length
## D = 0.19815, p-value = 1.532e-05
## alternative hypothesis: two-sidedks.test(iris$Sepal.Length, "pnorm",
mean = mean(iris$Sepal.Length),
sd = sd(iris$Sepal.Length))##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: iris$Sepal.Length
## D = 0.088654, p-value = 0.1891
## alternative hypothesis: two-sided
Aquí un ejemplo de cálculo de los restantes test de normalidad mencionados en la práctica. Recordad que es neceario que se cumplan los supuestos necesarios para poder utilizarlos (ver descripción de los tests al comienzo del documento).
Shapiro-Wilk
shapiro.test(iris$Petal.Width)##
## Shapiro-Wilk normality test
##
## data: iris$Petal.Width
## W = 0.90183, p-value = 1.68e-08Lilliefors
lillie.test(iris$Petal.Length)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: iris$Petal.Length
## D = 0.19815, p-value = 7.901e-16Jarque-Bera
jarque.bera.test(iris$Petal.Length)##
## Jarque Bera Test
##
## data: iris$Petal.Length
## X-squared = 14.023, df = 2, p-value = 0.0009013Anderson-Darling
ad.test(iris$Petal.Length)##
## Anderson-Darling normality test
##
## data: iris$Petal.Length
## A = 7.6785, p-value < 2.2e-16