En esta práctica trabajaremos sobre los SUPUESTOS que deben cumplirse a la hora de dar por válida una regresión lineal, concretamente los de LINEALIDAD, INDEPENDENCIA, NORMALIDAD y HOMOCEDASTICIDAD.

Estos supuestos proporcionan las bases para interpretar correctamente los resultados y las conclusiones del modelo.

La importancia de cumplir con estos supuestos radica en garantizar la validez de las inferencias estadísticas y las conclusiones derivadas del modelo de regresión. Además, el incumplimiento de estos supuestos puede afectar la capacidad predictiva del modelo y conducir a estimaciones sesgadas y poco fiables de los coeficientes de regresión. Es esencial realizar pruebas de diagnóstico para evaluar la violación de estos supuestos y, si es necesario, aplicar técnicas de corrección o considerar modelos

Aquí tenéis los enlaces a la publicación del documento de prácticas en RPubs y GitHUb. Los tests y gráficos de esta práctica se han realizado en el lenguaje de programación R. Consultar los documentos RMarkdown, y el .pdf para ver los ejemplos realizados y las explicaciones sobre los procedimientos.

Supuestos

• Linealidad: Este supuesto implica que la relación entre las variables independientes y la variable dependiente debe ser lineal. Si la relación es no lineal, los resultados de la regresión (lineal) pueden ser poco confiables y conducir a interpretaciones erróneas sobre la relación entre las variables.
• Normalidad: El supuesto de normalidad establece que los errores de la regresión deben seguir una distribución normal. ¡Cuidado con esto!, los errores, no las variables. Cuando este supuesto se cumple, las pruebas de hipótesis y los intervalos de confianza pueden interpretarse con mayor precisión. Si la normalidad no se cumple, los intervalos de confianza y las pruebas de hipótesis pueden verse afectados, lo que puede conducir a conclusiones erróneas.
• Homocedasticidad: Este supuesto implica que la varianza de los errores debe ser constante en todos los niveles de las variables predictoras. Cuando se viola este supuesto, se produce heterocedasticidad, lo que significa que la dispersión de los errores varía en diferentes rangos de las variables predictoras. La presencia de heterocedasticidad puede distorsionar los intervalos de confianza y los valores p-value, lo que puede afectar la precisión de las pruebas de hipótesis.
• Independencia: El supuesto de independencia indica que los errores de la regresión no deben estar correlacionados entre sí. Si hay autocorrelación presente, puede afectar la precisión de los coeficientes y las pruebas de hipótesis, lo que lleva a conclusiones erróneas sobre la importancia de las variables predictoras. ¿Qué es la autocorrelación? la presencia de autocorrelación en los residuos indica que los errores del modelo muestran cierto patrón sistemático en su distribución a lo largo del tiempo. Recordad que los errores o residuos de un modelo de regresión deberían distribuirse de manera aleatoria y seguir una distribución normal con media cero y varianza constante.

Dataset: mtcars

El conjunto de datos mtcars está integrado en R y contiene detalles, datos técnicos, y de rendimiento, sobre diferentes modelos de automóviles, recopilados por la revista “Motor Trend”. Se utiliza comúnmente como ejemplo en el aprendizaje y la práctica de análisis de datos y modelado en R. Cuenta con 32 observaciones para una lista de 11 variables.

data(mtcars)
head(mtcars)

##                    mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
## Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

str(mtcars)

## 'data.frame':    32 obs. of  11 variables:
##  $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
##  $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
##  $ disp: num  160 160 108 258 360 ...
##  $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
##  $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
##  $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
##  $ qsec: num  16.5 17 18.6 19.4 17 ...
##  $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
##  $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
##  $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
##  $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

Relación entre las variables

Antes de crear el modelo de regresión lineal, el que estudiaremos como variable dependiente o respuesta a mpg (miles per US gallon) e independiente o predictora weigth (wt), echaremos un vistazo a la relación existente entre ambas variables, gráficamente y, a nivel de correlación.

Si creamos un plot de ambas variables (x = wt, y = mpg) podemos ver como hay una relación negativa entre ellas. Como era de esperar, un aumento del peso del vehículo dará lugar a una disminución del rendimiento en lo que se refiere al consumo de combustible. Los vehículos más pesados recorrerán menos millas por galón de combustible.

par(mfrow = c(1, 1))
plot(mtcars$wt, mtcars$mpg,
     main = "millas por gallon VS weigth",
     sub = "plot",
     xlab = "peso",
     ylab = "millas por galón",
     cex.lab = 1.2,
     cex.axis = 1,
     mgp = c(2.4, 1, 0),
     pch = 19,
     col = "black")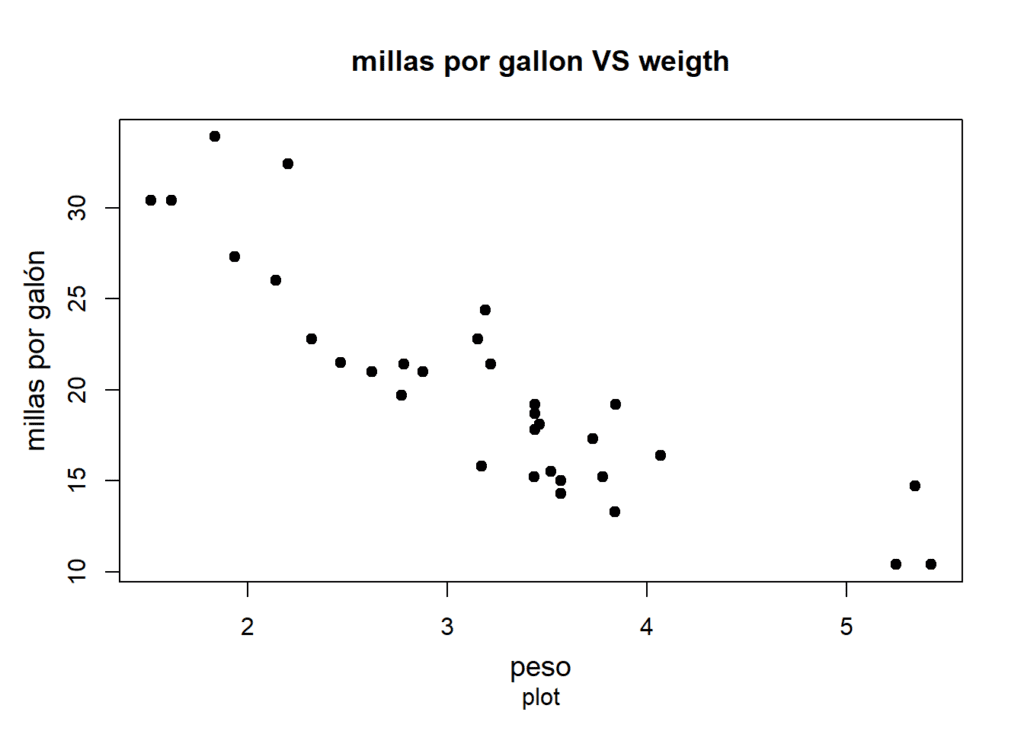

Podemos cuantificar esa relación negativa midiendo su correlación lineal (-0,87, correlación fuerte).

df <- data.frame(mtcars$mpg, mtcars$wt)
colnames(df) <- c("peso", "millas/galón")
pairs.panels(df, method = "pearson",
             main = "Correlación mpg / wt",
             cex.labels = 1.5,
             cex.cor = 1, stars = TRUE,
             pch = 20,
             gap = 0, 
             lm = TRUE, col = "#2ECC71", 
             hist.col = "#2ECC71")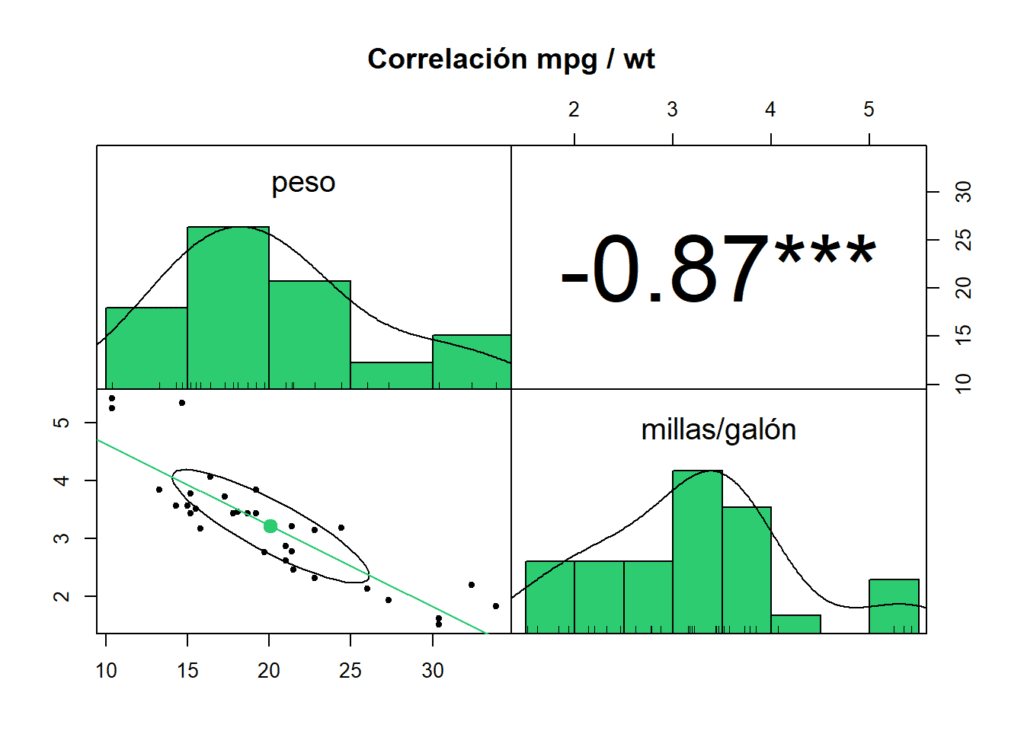

También podemos estudiar esta correlación con la función cor. La Ho (nula) es que no existe correlación entre las variables. El resultado sugiere que existe una fuerte correlación entre el peso del automóvil y la eficiencia del combustible en términos de millas por galón. Un valor de p tan bajo indica una alta significancia estadística, lo que respalda descartar la Ho y aceptar la alternativa, que señala la presencia de una relación entre estas dos variables.

cor.test(mtcars$wt, mtcars$mpg)

## 
##  Pearson's product-moment correlation
## 
## data:  mtcars$wt and mtcars$mpg
## t = -9.559, df = 30, p-value = 1.294e-10
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.9338264 -0.7440872
## sample estimates:
##        cor 
## -0.8676594

Regresión lineal

Creamos el modelo de regresión lineal con la función lm. El modelo resultante sería igual a mpg = -5,3445 wt + 37,2851, con un coeficiente de determinación R^2 ajustado de 0,7446 Con este modelo, el 74,46% de la varianza en mpg sería explicada por wt.

mod <- lm(mpg ~ wt, data = mtcars) # mpg ~ wt
summary(mod)

## 
## Call:
## lm(formula = mpg ~ wt, data = mtcars)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.5432 -2.3647 -0.1252  1.4096  6.8727 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  37.2851     1.8776  19.858  < 2e-16 ***
## wt           -5.3445     0.5591  -9.559 1.29e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.046 on 30 degrees of freedom
## Multiple R-squared:  0.7528, Adjusted R-squared:  0.7446 
## F-statistic: 91.38 on 1 and 30 DF,  p-value: 1.294e-10

Comprobación supuestos

Linealidad

Una forma de comprobar la linealidad es ver si la media de los residuos del modelo es igual, o cercana, a 0. En este caso, se cumple, con una media de prácticamente 0.

mean(mod$residuals)

## [1] 7.196392e-17

Normalidad

Para comprobar la normalidad vamos a utilizar el test de Shapiro-Wilk, dado que el número de observaciones es inferior a 50 (idealmente, entre 30 y 50; n = 35). Con un p-value de 0.1044 (mayor que 0,05) no descartamos la Ho de normalidad.

shapiro.test(mod$residuals)

## 
##  Shapiro-Wilk normality test
## 
## data:  mod$residuals
## W = 0.94508, p-value = 0.1044

Al mismo tiempo, utilizamos un gráfico QQ-PLOT para valorar la normalidad visualmente. En un gráfico Q-Q, los cuantiles de la muestra se comparan con los cuantiles teóricos de la distribución de interés. Si los puntos en el gráfico se ajustan aproximadamente a una línea diagonal, indica que los datos siguen de cerca la distribución teórica (normal). Para hacer este gráfico utilizamos la fuciones qqplot y qqline.

qqPlot(mod$residuals, 
       distribution = "norm",
       main = "Q-Q PLOT de residuos en mpg ~ wt",
       xlab = "cuantiles teóricos",
       ylab = "cuantiles de la muestra",
       id = FALSE, grid = TRUE,
       envelope = 0.95, col = carPalette()[1], col.lines = carPalette()[3],
       pch = 20,
       cex = 1,
       lwd = 2)
qqline(mod$residuals,
       col = "blue",
       lty = 1,
       lwd = 2)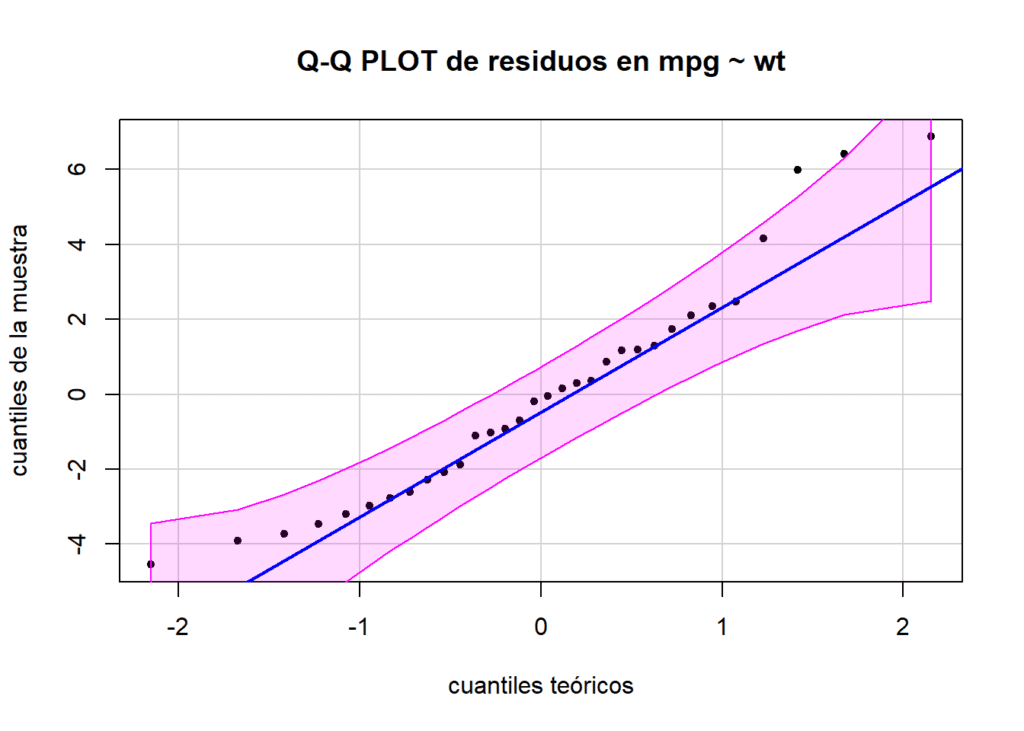   

Homocedasticidad

Para evaluar la homocedasticidad de los residuos utilizamos el test de Breusch-Pagan, con la función bptest() La función captura los residuos guardados en el objeto mod para realizar los cálculos, por lo que no es necesario indicarlo de la forma mod$residuals

bptest(mod)

## 
##  studentized Breusch-Pagan test
## 
## data:  mod
## BP = 0.040438, df = 1, p-value = 0.8406

Igualmente, podemos evaluar la homocedasticidad de forma visual utilizando plot del objeto mod. Tenemos dos gráficos para ver esto: (gráfico 1) la distribución de los residuos VS valores ajustados. Lo que se busca es que estos presenten un patrón aleatorio alrededor de 0. Un patrón aleatorio sugiere que el modelo de regresión es apropiado y que los supuestos del modelo se cumplen. Por otro lado, el (gráfico 2), donde los residuos están estandarizados en términos de su error estándar. Un gráfico de residuos estandarizados versus valores ajustados es útil para identificar valores atípicos y puntos influyentes que se destacan en términos de su distancia con respecto a los valores ajustados y su variabilidad. La estandarización de los residuos los convierte en valores adimensionales, lo que facilita la comparación de la magnitud de los residuos en diferentes partes del rango de valores ajustados. En este caso los gráficos muestran una cierta pérdida de homocedasticidad, mientras que el test validó esta.

par(mfrow = c(1, 2))
plot(mod, 1)
plot(mod, 3)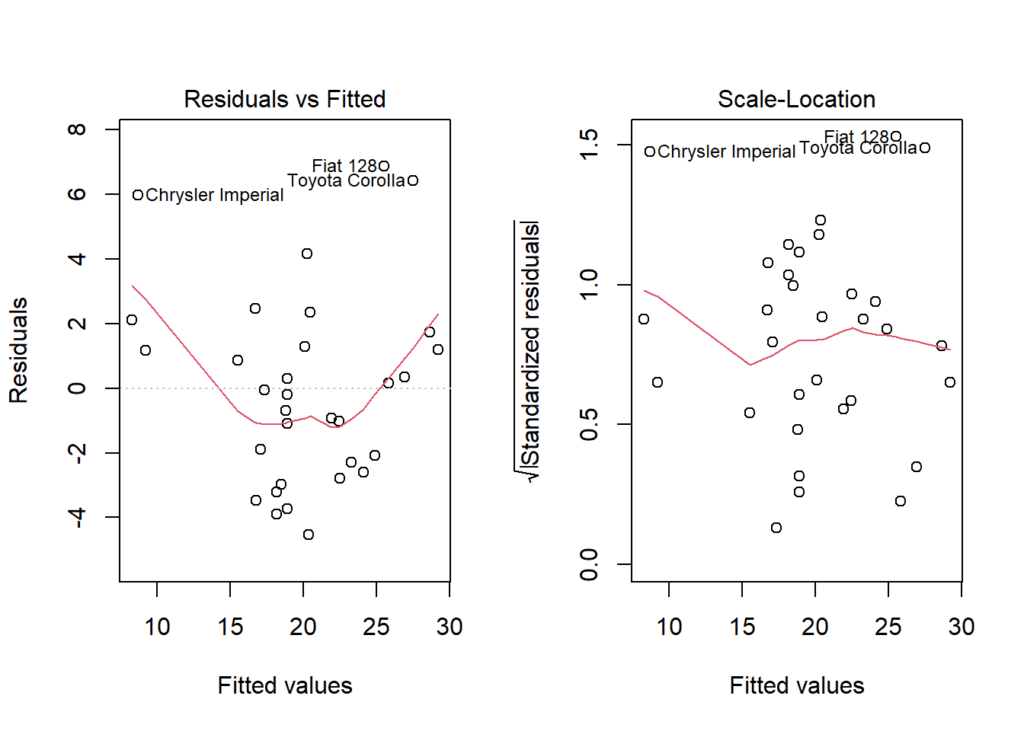

Independencia

El test de Durbin-Watson es una prueba estadística que se utiliza para analizar la presencia de autocorrelación de primer orden en los residuos de un modelo de regresión. Aunque su uso original estaba destinado a modelos de regresión lineal simple, también puede aplicarse a modelos de regresión múltiple. La prueba proporciona información sobre la independencia de los residuos. El estadístico de Durbin-Watson toma valores entre 0 y 4. Un valor de 2 sugiere que no hay autocorrelación. Los valores más cercanos a 0 indican autocorrelación positiva, mientras que los valores más cercanos a 4 indican autocorrelación negativa.

El p-value es inferior a 0,05, por lo que se descarta la H0 de ausencia de autocorrelación en los residuos. El valor del estadístico de D-W es de 1,25. Habría que aceptar la H alternativa de que hay “autocorrelación” y por tanto, no hay independencia en los residuos. Este resultado hace que tengamos que ser precavidos con el modelo generado.

durbinWatsonTest(mod)

##  lag Autocorrelation D-W Statistic p-value
##    1       0.3628798      1.251727   0.016
##  Alternative hypothesis: rho != 0