t-student en R.

Esta práctica puede consultarse en el repositorio RPubs. https://rpubs.com/acastro/1213002

¿QUÉ ES LA T DE STUDENT?

La conocida como “t de Student” es una prueba estadística que se utiliza para comparar las medias de una o dos muestras con el objetivo de determinar si hay evidencia significativa de que las medias son diferentes entre sí. Dependiendo de la situación, se pueden usar diferentes variantes de la prueba t.

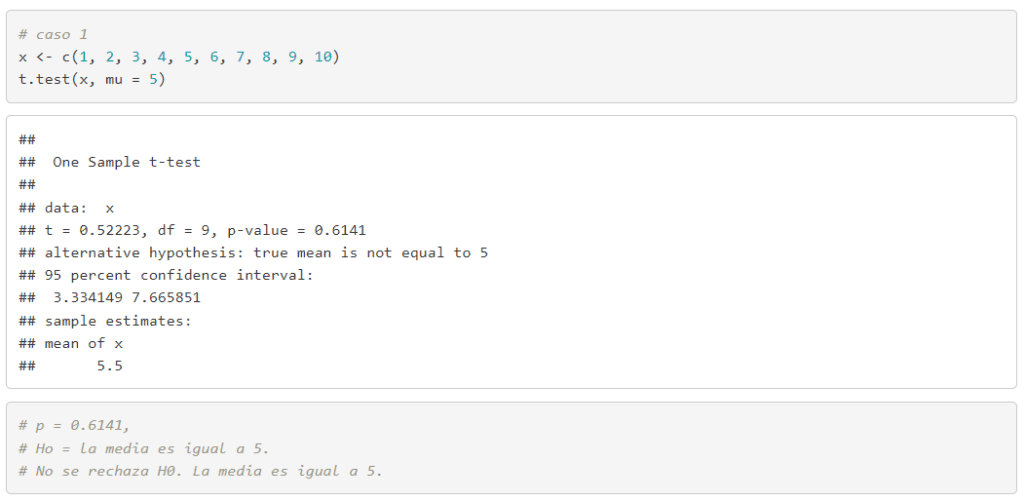
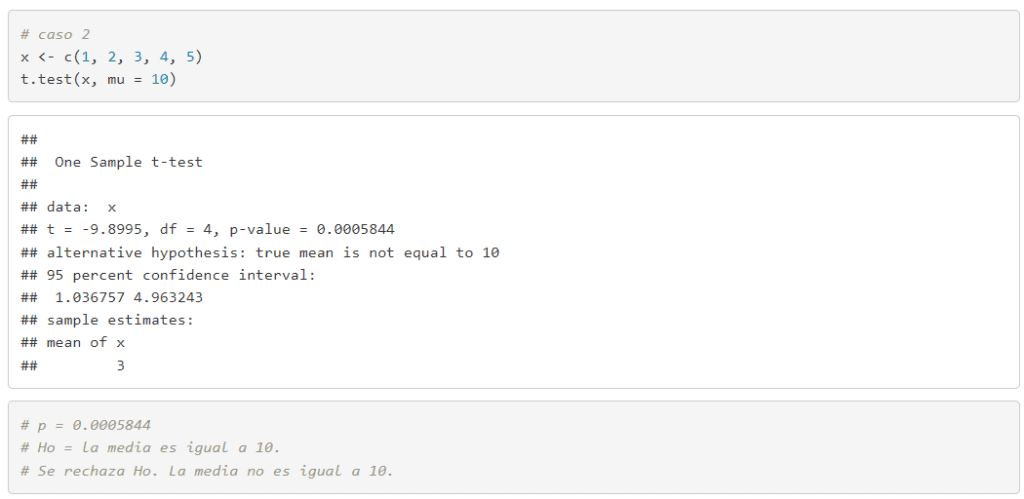
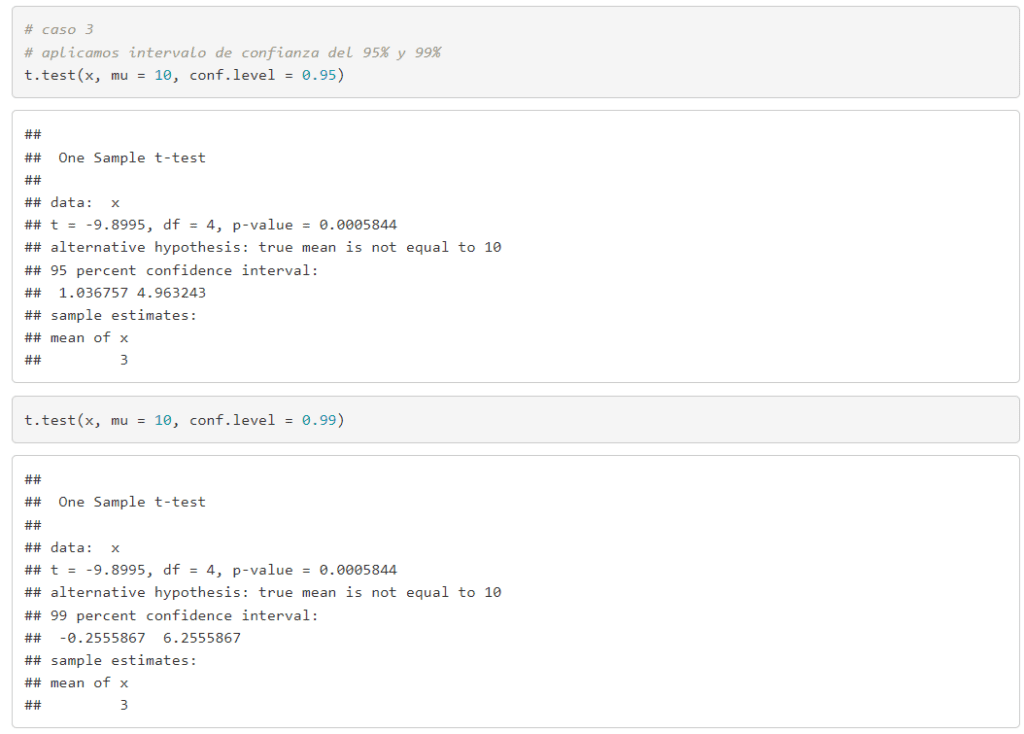
1. Prueba t para una muestra. Determinar si la media de una muestra es significativamente diferente de un valor específico, que generalmente es una media teórica o conocida de la población.
2. Prueba t para dos muestras independientes. Comparar las medias de dos muestras independientes para ver si hay una diferencia significativa entre ellas.
3. Prueba t para muestras pareadas. Comparar las medias de dos muestras relacionadas o pareadas, como las medidas antes y después en el mismo grupo de sujetos.
4. Pruebas de hipótesis. Se utiliza comúnmente en pruebas de hipótesis donde la hipótesis nula (H0) afirma que no hay diferencia entre las medias, y la hipótesis alternativa (H1) sugiere que sí la hay.

SUPUESTOS

NORMALIDAD

Prueba t para una muestra: Los datos deben provenir de una población que sigue una distribución normal. Este supuesto es especialmente importante cuando el tamaño de la muestra es pequeño (n < 30). Sin embargo, si la muestra es grande, la prueba t es robusta frente a desviaciones moderadas de la normalidad.

Prueba t para dos muestras independientes: Se asume que ambas poblaciones de las que provienen las muestras siguen una distribución normal.

• Test de Shapiro-Wilk. Muestras pequeñas/medianas (3 a 50 muestras).
• Test de Kolmogorov-Smirnov (K-S). Adecuado para muestras grandes (50 a 100). Tamaños más grandes pueden detectar desviaciones de la normalidad que no resultan prácticas.
• Test de Lilliefors. Una variación del test de Kolmogorov-Smirnov ajustada para distribuciones con media y desviación estándar desconocidas.
• Test de Anderson-Darling. Cualquier tamaño de muestra. Evalúa la adecuación de la muestra a una distribución normal y es más sensible en los extremos de la distribución.
• Test de Jarque-Bera. Más común en muestras grandes (de 50 a 100). Basado en los momentos de la distribución (asimetría y curtosis) para evaluar la normalidad.
• Histograma. Visualizar la distribución de los datos para evaluar si se asemeja a una distribución normal.
• Gráfico Q-Q (Quantile-Quantile). Comparar los cuantiles de la muestra con los cuantiles de una distribución normal. Los puntos deben seguir aproximadamente una línea recta. Desviaciones significativas de esta línea indican desviaciones de la normalidad.
• Gráfico P-P (Probability-Probability). Similar al gráfico Q-Q, compara las probabilidades acumuladas de la muestra con las de una distribución normal. Los puntos deben alinearse a lo largo de la línea diagonal.

HOMOCEDASTICIDAD

Prueba t para dos muestras independientes: Se asume que las varianzas de las dos poblaciones son iguales (homocedasticidad). Existen variantes de la prueba t que no requieren este supuesto (por ejemplo, la prueba t de Welch), pero la prueba t estándar lo presupone.

• Test de Bartlett. Evaluar si las varianzas de dos o más grupos son iguales. Es más sensible a la normalidad de los datos en comparación con el test de Levene. Un valor p bajo indica que las varianzas entre los grupos son significativamente diferentes, lo que sugiere heterocedasticidad.
• Test de Levene. Evaluar la igualdad de varianzas entre dos o más grupos. Es menos sensible a las desviaciones de la normalidad en comparación con el test de Bartlett.Un valor p bajo (por debajo del nivel de significancia, como 0.05) indica que las varianzas entre los grupos son significativamente diferentes,lo que sugiere heterocedasticidad.
• Test de Fligner-Killeen. Evaluar la igualdad de varianzas entre dos o más grupos, especialmente cuando los datos no se distribuyen normalmente.Menos sensible a las desviaciones de la normalidad y más robusto en presencia de datos que no cumplen con el supuesto de normalidad.

INDEPENDENCIA

Las observaciones deben ser independientes unas de otras, es decir, el valor de una observación no debe influir en el valor de otra. Este supuesto es crucial en todas las variantes de la prueba t (una muestra, dos muestras independientes, muestras pareadas).

VARIABLES CONTINUAS

Escala de Medición. La variable dependiente debe ser continua (es decir, debe estar medida en una escala de intervalo o de razón).

ALEATORIEDAD

Los datos deben haber sido seleccionados de manera aleatoria de la población, lo que ayuda a garantizar que las conclusiones sean generalizables a toda la población.

PRUEBA T PARA UNA MUESTRA

PRUEBA T PARA DOS MUESTRAS INDEPENDIENTES

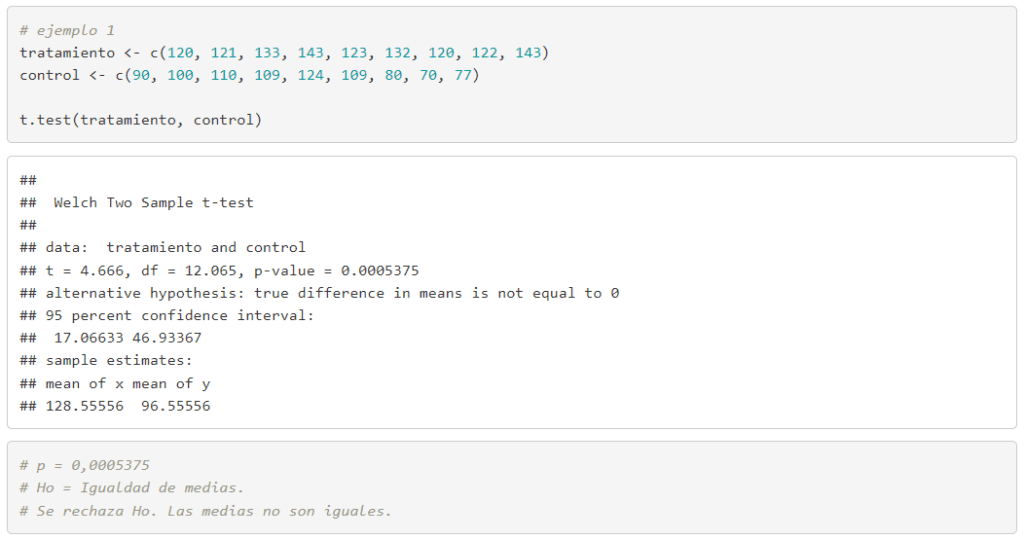
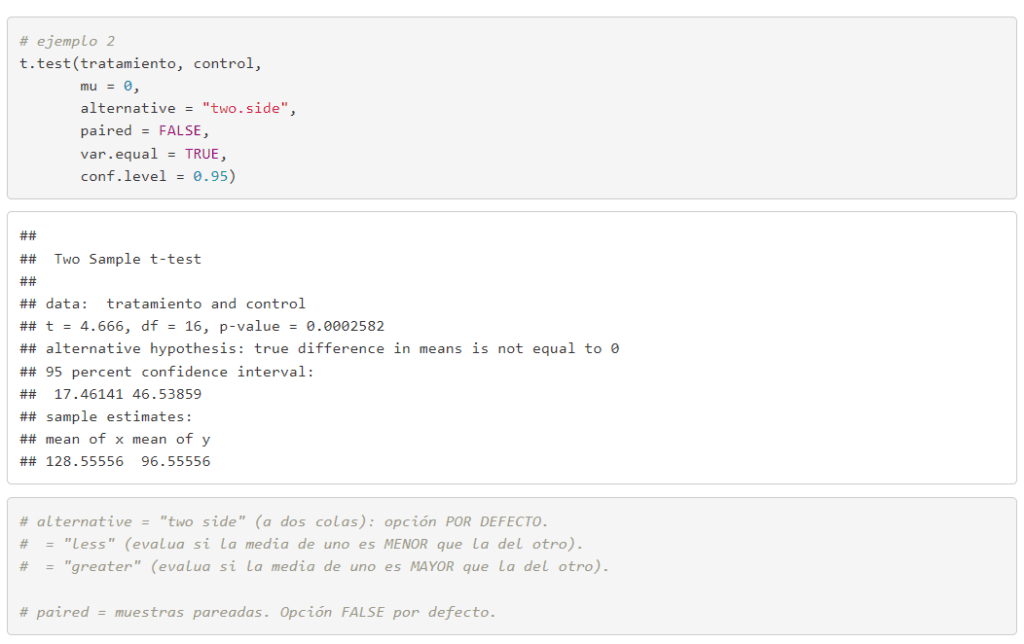
Parámetros obtenidos

CON DATOS EN COLUMNAS DE UN DATA FRAME

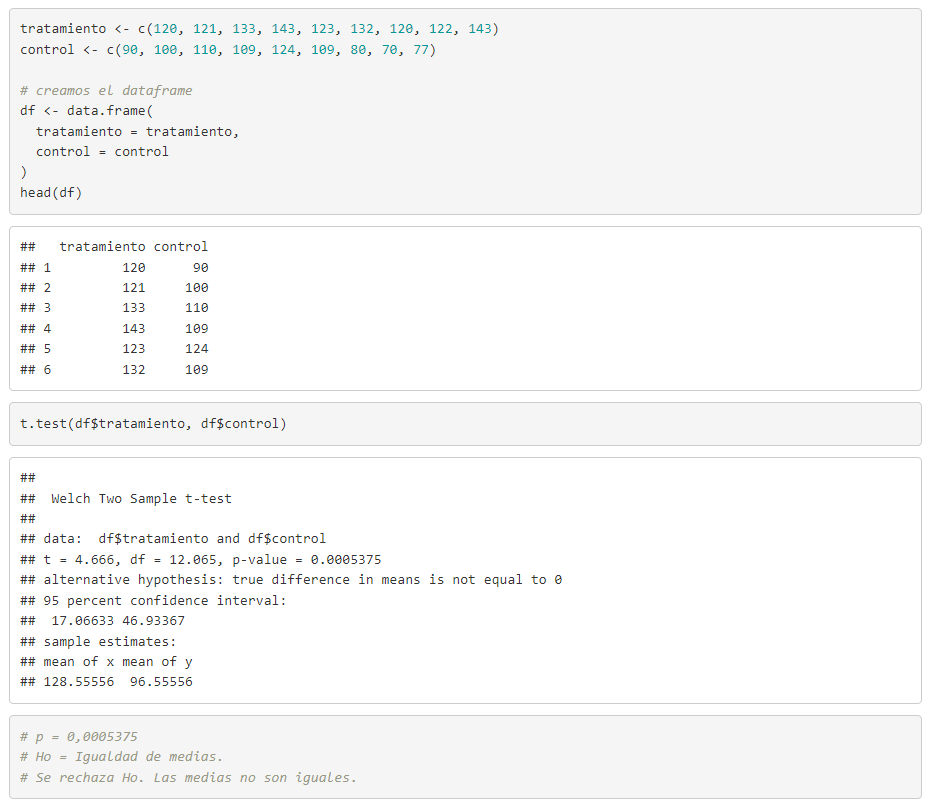
CON DATOS SITUADOS EN FILAS DE UN DATA FRAME

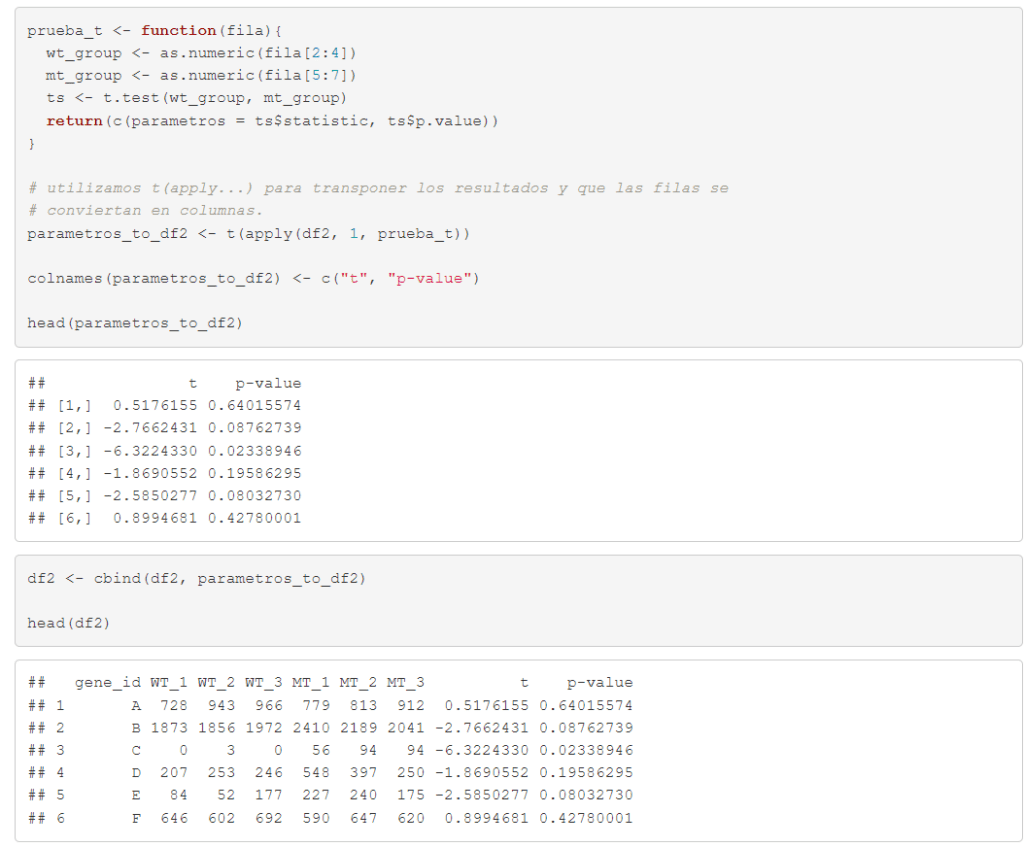
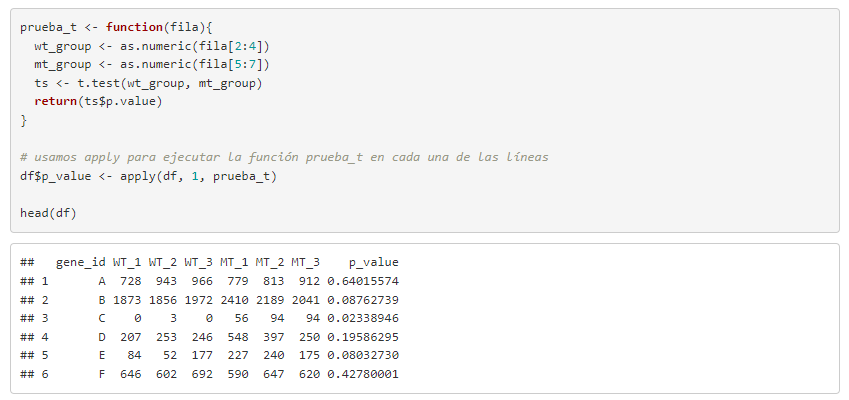
En ocasiones es necesario calcular algo donde se requiere utilizar los datos o valores que están situados a lo largo de las filas del dataframe, y no en columnas. En esta práctica creamos una función (prueba_t) que nos permite (1) agrupar las muestras wt y mt para cada una de las filas y (2) realizar un test de t-student a estos grupos creados. Estudiamos así la igualdad de medias entre ambos grupos, para cada fila y, añadimos al dataframe el p_value obtenido.

Partimos del siguiente dataframe, en el que se identifican una serie de genes (genes_id), con nombres A, B, C… y unos valores para las variables WT_1, WT_2, WT_3 y MT_1, MT_2, MT_3.

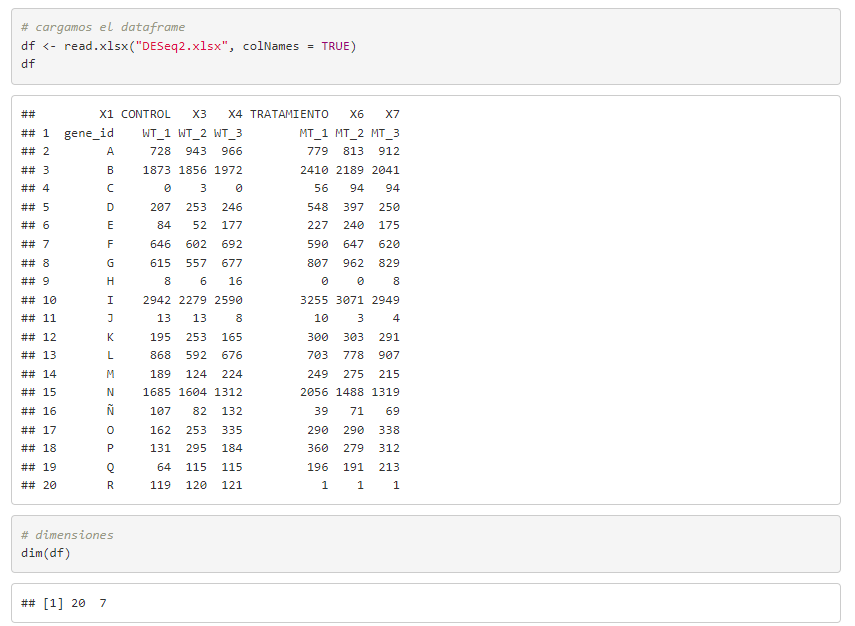
Tras realizar algunos arreglos, continuamos con la siguiente (ver el proceso completo en el documento de la práctica publicada en RPubs).

La función prueba_t crea dos grupos (wt y mt) con las diferentes variables wt y mt del dataframe y, calcula el test t-student para estudiar la igualdad de medias entre ellas. Tras realizar el test, la función devuelve el valor del p-value obtenido. Como nos interesa hacer esto para cada una de las filas, usamos la función de apply de R. Con esta función podemos llamar a prueba_t para que se ejecute en cada una de las líneas del dataframe. Con el código df$p_value <- creamos la nueva variable p_value, donde se almacenará el valor del p valor obtenido con cada prueba t-student realizada para comparar la media entre los grupos. La tabla muestra ya los p_values añadidos.

Si queremos añadir a un dataframe dos o más parámetros, podemos hacerlo de la forma que vamos a ver en este ejemplo (en este caso concreto vamos a añadir el valor del estadístico (t) y el p-value). La función prueba_t devolverá un vector con estos dos valores y con la función apply haremos que se ejecute la prueba para los grupos wt y mt de cada una de las líneas.